Инструкция
1
Сформулируйте проблему. Она должна существовать в настоящем, а не в прошлом или будущем. Формулируйте конкретно, избегая лишних слов. Старайтесь на затрагивать глобальные проблемы, повлиять на которые практически невозможно («глобальное потепление», «бездуховность общества» и т.д.).
2
Составьте перечень заинтересованных лиц. То есть, необходимо выявить всех участников, которых прямо или косвенно касается данная проблема. Для этого нужно ответить на следующие вопросы. На кого эта проблема оказывает самое большое воздействие? Кто будет непосредственно участвовать в решении проблемы? Какие организации или группы людей могут оказать влияние на ход работы? Установите, каким именно образом то или иное заинтересованное лицо зависит от проблемы.

3
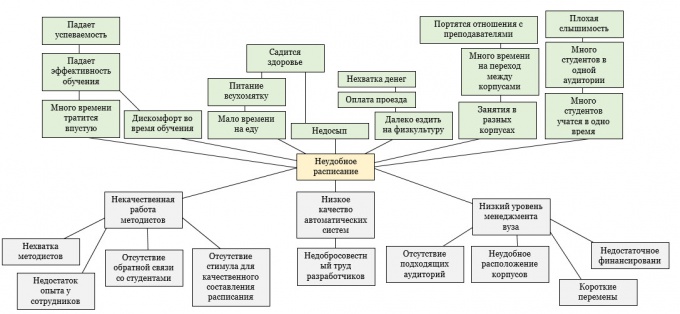
Начните строить дерево проблем. Оно состоит из трех частей: корней, ствола и кроны. Корни – это причины, из-за которых возникла проблема. Именно они обусловливают ее существование. Если их устранить, проблема исчезнет. Ствол – формулировка. Крона – это любые последствия, которые повлекла за собой проблема. Сначала нарисуйте ствол.
4
Далее необходимо нарисовать корни. Сначала выпишите все причины, которые возникнут у вас в ходе мозгового штурма. Затем сгруппируйте их и укажите взаимосвязи. Постарайтесь найти максимальное число «корней», так как именно их решение окажет решающее воздействие.
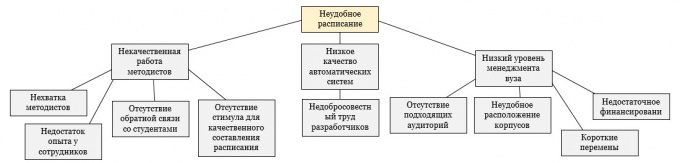
5
Последний пункт – крона. Определите непосредственные точки соприкосновения проблемы и последствий. Затем отследите, какое еще негативное влияние может быть оказано, то есть спуститесь на уровень ниже. Продолжайте делать это до тех пор, пока последствия еще входят в рамки проблемы.
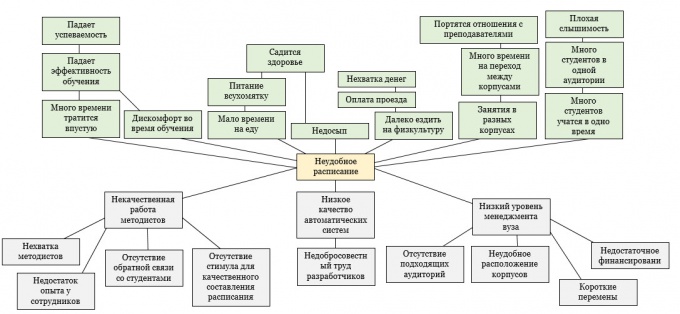
Обратите внимание
Часто вместо одной проблемы анализируются несколько. Допустим, вместо "увеличения эффективности производства деталей" рассматривают просто "увеличение эффективности". Старайтесь этого избегать и брать максимально низкий уровень.
Полезный совет
Дерево проблем проще всего строить в команде, используя разрезанные квадраты из бумаги. Каждому участнику выделите роль заинтересованного лица и попросите его написать на отдельном листе бумаги ключевое утверждение. В конце соедините все вместе и получите готовую модель. Проанализируйте недочеты и исправьте их.