Инструкция
1
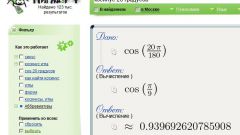
Если известна величина интересующего вас острого угла, то вычисление сведется к нахождению значения косинуса с помощью любого калькулятора или онлайн-вычислителя. Если вы выберите калькулятор, то используйте, например, встроенную в ОС Windows программу этого рода. Она запускается через главное меню на кнопке «Пуск», в котором ссылка «Калькулятор» помещена в подраздел «Служебные» раздела «Стандартные», открываемого выбором в меню пункта «Все программы».
2
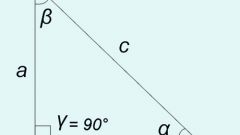
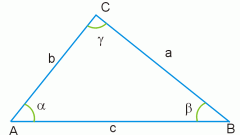
Если известна величина не того угла, косинус которого требуется вычислить, а угла, примыкающего к противоположному концу гипотенузы, то исходите из того, что в евклидовой геометрии сумма всех углов треугольника всегда равна 180°. Используя эту классическую теорему вычислите нужный угол - отнимите от 180° известный угол и угол прямой (90°). После этого исходные данные и метод вычисления совпадут с теми, что описаны в предыдущем шаге.
3
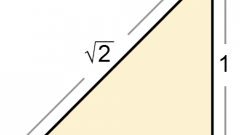
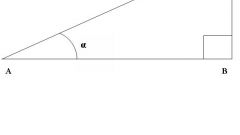
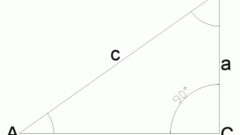
Если величины острых углов прямоугольного треугольника неизвестны, но есть данные о длинах его сторон, то для нахождения значения косинуса нужного угла задействуйте базовое определение этой тригонометрической функции. Оно утверждает, что косинус острого угла равен соотношению длин катета и гипотенузы, образующих этот угол.
4
Если длина именно того катета, который прилегает к нужному углу, неизвестна, то ее можно рассчитать, исходя из теоремы Пифагора, а затем прибегнуть к методу, описанному в предыдущем шаге. Как вы наверняка помните, эта теорема утверждает, что сумма квадратов длин катетов прямоугольного треугольника всегда равна квадрату длины его гипотенузы. Поэтому для вычисления длины недостающей стороны найдите квадратный корень из разности между квадратами длин гипотенузы и известного катета, а затем действуйте так, как описано в предыдущем шаге.
5
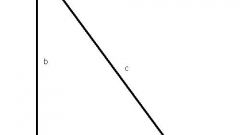
Если неизвестна длина гипотенузы, то используйте ту же самую теорему - найдите значение квадратного корня из суммы возведенных в квадрат длин катетов и возвращайтесь к методу, описанному в третьем шаге.
Видео по теме