Вам понадобится
- -циркуль
- -карандаш
- -линейка
- -лист бумаги
Инструкция
1
Для построения необходимо найти внутри многоугольника центр вписанной окружности и определить ее радиус. Вписать окружность можно не в каждый многоугольник. Уточните, позволяют ли свойства заданной фигуры вписать в нее окружность. Не получится вписать окружность в произвольный неправильный многоугольник, не имеющий ни одной оси симметрии.
2
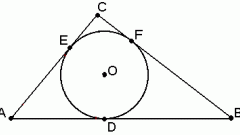
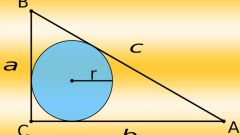
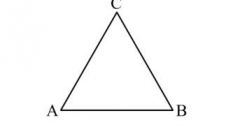
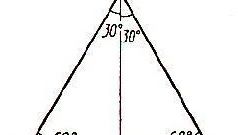
В любом треугольнике можно построить вписанную окружность, и эта окружность будет единственной для данного треугольника. Ее центр находится в точке пересечения биссектрис треугольника, поскольку именно биссектриса является геометрическим местом точек, одинаково удаленных от сторон угла.
3
Для нахождения центра вписанной окружности сделайте из тонкой бумаги копию заданного треугольника. Аккуратно сложите этот вспомогательный треугольник сторона к стороне от одной вершины. Линия сгиба разделит угол при вершине пополам. Повторите сложение от двух других вершин. Точка пересечения линий сгибов и будет центром вписанной окружности. Наложите копию на заданный треугольник и иглой циркуля поставьте точку центра. Для нахождения радиуса вписанной окружности опустите перпендикуляр на любую сторону треугольника. Полученным радиусом начертите окружность.
4
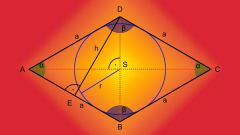
Из четырехугольников окружность можно вписать лишь в те, у которых суммы противоположных сторон равны. Под это условие подходят любые квадраты, ромбы и трапеции с определенными параметрами. В квадрате и ромбе центр вписанной окружности лежит в точке пересечения диагоналей. Радиус равен половине стороны квадрата или перпендикуляру, опущенному из центра на любую сторону ромба.
5
В трапеции радиус очевидно равен половине высоты. Центр лежит на средней линии трапеции. Для нахождения центра достаточно провести биссектрису любого угла трапеции до пересечения со средней линией.
6
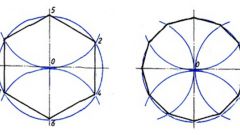
В любой правильный многоугольник можно вписать окружность. Центр такой окружности лежит в точке пересечения биссектрис, а радиус равен перпендикуляру из центра на любую сторону.
Видео по теме