Вам понадобится
- - свойства симметричных точек;
- - свойства симметричных фигур;
- - линейка;
- - угольник;
- - циркуль;
- - карандаш;
- - лист бумаги;
- - компьютер с графическим редактором.
Инструкция
1
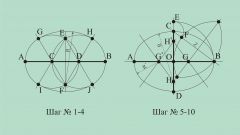
Проведите прямую a, которая будет являться осью симметрии. Если ее координаты не заданы, начертите ее произвольно. С одной стороны от этой прямой поставьте произвольную точку A. необходимо найти симметричную точку.
2
Вспомните, какие точки являются симметричными относительно оси. Прямая a в этом случае должна являться серединным перпендикуляром к отрезку между этими точками. То есть для того, чтобы определить местоположение точки В, необходимо провести от точки А перпендикуляр к оси симметрии и продолжить его. Точку пересечения оси и перпендикуляра к ней обозначьте как О.
3
От точки О отложите расстояние, равное отрезку ОА. Поставьте точку В. Она будет симметрична точке А. Если задана находящаяся на плоскости прямая А, то каждая точка, находящаяся по одну ее сторону, симметрична всего одной точке, находящейся по другую сторону от этой прямой. Представьте себе вращение плоскости вокруг данного отрезка. Если она повернется на 180°, то точки А и В поменяются местами.
4
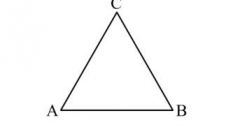
Точно таким же образом можно построить и две симметричные геометрические фигуры. Например, задан треугольник ABC, к которому необходимо построить симметричный. Проведите ось симметрии. Она может быть задана условиями задачи. Их каждой вершины заданного треугольника проведите к этой прямой перпендикуляры и продлите их на другую сторону плоскости. Обозначьте точки пересечения как О, О1 и О2. От каждой из этих точек отложите отрезки, равный ОА, О1В и О2С. Соедините полученные точки прямыми. Точно так же можно начертить и другие пары симметричных фигур.
Полезный совет
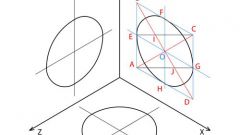
Свойства симметрии постоянно используются в программе AutoCAD. Для этого используется опция Mirror. Для построения равнобедренного треугольника или равнобедренной трапеции достаточно начертить нижнее основание и угол между ним и боковой стороной. Отразите их с помощью указанной команды и продлите боковые стороны до необходимой величины. В случае с треугольником это будет точка их пересечения, а для трапеции — заданная величина.
С симметрией вы постоянно сталкиваетесь в графических редакторах, когда пользуетесь опцией «отразить по вертикали/горизонтали». В этом случае за ось симметрии берется прямая, соответствующая одной из вертикальных или горизонтальных сторон рамки рисунка.
С симметрией вы постоянно сталкиваетесь в графических редакторах, когда пользуетесь опцией «отразить по вертикали/горизонтали». В этом случае за ось симметрии берется прямая, соответствующая одной из вертикальных или горизонтальных сторон рамки рисунка.
Источники:
- как начертить центральную симметрию