Инструкция
1
Прямым называется параллелепипед, у которого четыре боковые грани - прямоугольники. Для вычисления объема нужно площадь основания умножить на высоту - V=Sh. Предположим, основание прямого параллелепипеда - параллелограмм. Тогда площадь основания будет равна произведению его стороны на высоту, проведенную к этой стороне - S=aс. Тогда V=ach.
2
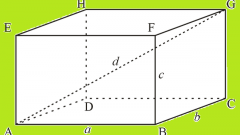
Прямоугольным называется прямой параллелепипед, у которого все шесть граней - прямоугольники. Примеры: кирпич, спичечная коробка. Для вычисления объема нужно площадь основания умножить на высоту - V=Sh. Площадь основания в данном случае - это площадь прямоугольника, то есть произведение величин двух его сторон - S=ab, где a - ширина, b - длина. Итак, получаем искомый объем - V=abh.
3
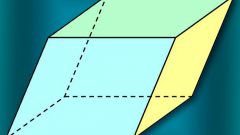
Наклонным называется параллелепипед, боковые грани которого не перпендикулярны граням основания. В этом случае объем равен произведению площади основания на высоту - V=Sh. Высота наклонного параллелепипеда - перпендикулярный отрезок, опущенный из любой верхней вершины на соответствующую сторону основания боковой грани (то есть высота любой боковой грани).
4
Кубом называется прямой параллелепипед, у которого все ребра равны, а все шесть граней являются квадратами. Объем равен произведению площади основания на высоту - V=Sh. Основание - квадрат, площадь основания которого равна произведению двух его сторон, то есть величина стороны в квадрате. Высота куба - та же величина, поэтому в данном случае объемом будет величина ребра куба, возведенная в третью степень - V=a³.