Инструкция
1
Прежде всего нужно установить, определена ли заданная функция на всем отрезке [a, b] и если у нее есть точки разрыва, то какого рода эти разрывы. Например, функция f(x) = 1/x вовсе не имеет ни максимального, ни минимального значения на отрезке [-1, 1], поскольку в точке x = 0 стремится к плюс бесконечности справа и к минус бесконечности слева.
2
Если заданная функция — линейная, то есть задана уравнением вида y = kx + b, где k ≠ 0, то она на всей своей области определения монотонно возрастает, если k > 0; и монотонно убывает, если k 0; и f(a), если k
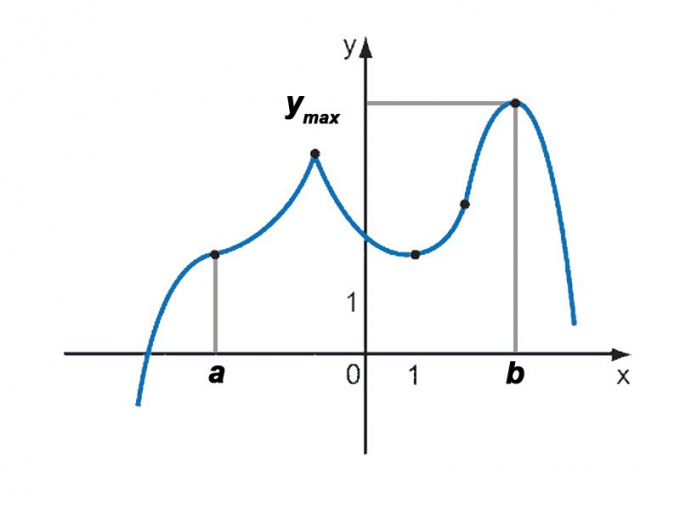
Следующий шаг — исследование функции на экстремумы. Даже если установлено, что f(a) > f(b) (или наоборот), функция может достигать больших значений в точке максимума.

Чтобы найти точку максимума, необходимо прибегнуть к помощи производной. Известно, что если в точке x0 функция f(x) имеет экстремум (то есть максимум, минимум или стационарную точку), то ее производная f′(x) в этой точке обращается в ноль: f′(x0) = 0.

Для определения, какой из трех видов экстремума находится в обнаруженной точке, нужно исследовать поведение производной в ее окрестностях. Если она меняет знак с плюса на минус, то есть монотонно убывает, то в найденной точке исходная функция имеет максимум. Если производная меняет знак с минуса на плюс, то есть монотонно возрастает, то в найденной точке исходная функция имеет минимум. Если же, наконец, производная не меняет знака, то x0 — это стационарная точка для исходной функции.

В тех случаях, когда вычислить знаки производной в окрестностях найденной точки сложно, можно воспользоваться второй производной f′′(x) и определить знак этой функции в точке x0:

- если f′′(x0) > 0, то найдена точка минимума;
- если f′′(x0)
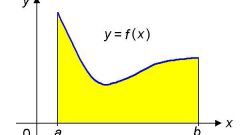
Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.

3
Следующий шаг — исследование функции на экстремумы. Даже если установлено, что f(a) > f(b) (или наоборот), функция может достигать больших значений в точке максимума.
4
Чтобы найти точку максимума, необходимо прибегнуть к помощи производной. Известно, что если в точке x0 функция f(x) имеет экстремум (то есть максимум, минимум или стационарную точку), то ее производная f′(x) в этой точке обращается в ноль: f′(x0) = 0.

Для определения, какой из трех видов экстремума находится в обнаруженной точке, нужно исследовать поведение производной в ее окрестностях. Если она меняет знак с плюса на минус, то есть монотонно убывает, то в найденной точке исходная функция имеет максимум. Если производная меняет знак с минуса на плюс, то есть монотонно возрастает, то в найденной точке исходная функция имеет минимум. Если же, наконец, производная не меняет знака, то x0 — это стационарная точка для исходной функции.
5
В тех случаях, когда вычислить знаки производной в окрестностях найденной точки сложно, можно воспользоваться второй производной f′′(x) и определить знак этой функции в точке x0:

- если f′′(x0) > 0, то найдена точка минимума;
- если f′′(x0)
Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.
6
Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.