Вам понадобится
- Линейка без делений, циркуль, транспортир
Инструкция
1
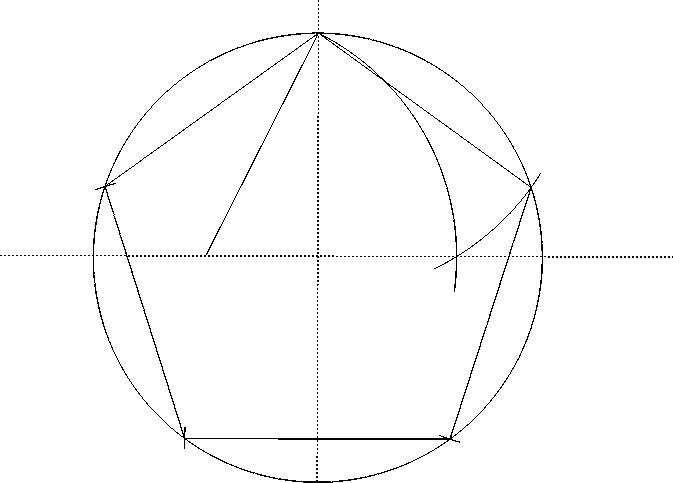
Постройте окружность с центром в некоторой точке О произвольного радиуса. Через центр окружности проводим ее диаметр, назовите его, например АВ. Постройте еще один диаметр этой окружности, перпендикулярный диаметру АВ. Для этого проведите из точек А и В две окружности с радиусами, большими чем радиус построенной окружности. Через точки в месте их пересечения, и через точку О проведите диаметр, перпендикулярный диаметру АВ. Назовем его СD.
С помощью подобного построения, проводя окружность из точек А и О, постройте точку Е, которая является серединой отрезка АО. Радиусом СЕ, из центра в точке Е, проведите окружность и найдите точку ее пересечения с отрезком АВ. На пересечении поставим точку F.
С помощью подобного построения, проводя окружность из точек А и О, постройте точку Е, которая является серединой отрезка АО. Радиусом СЕ, из центра в точке Е, проведите окружность и найдите точку ее пересечения с отрезком АВ. На пересечении поставим точку F.
2
Полученный отрезок CF и является стороной пятиугольника, который вписан в проведенную окружность. Циркулем возьмите отрезок CF. Пусть первая точка деления, будет С. Проведите из нее радиусом CF окружность до пересечения с делимой окружностью. Из полученной точки снова проведите окружность тем же радиусом, до нового пересечения с окружностью. Повторите эту операцию еще два раза. В результате на окружности появится пять точек, которые и являются вершинами вписанного в нее правильного пятиугольника.
Дуги между полученными точками будут равны, а значит, окружность разделена на пять равных частей. После этого можно поделить круг. Для этого из точки О проведите отрезки к точкам, делящим окружность. В результате получится пять секторов одинаковой площади, которые делят круг на равные части.
Дуги между полученными точками будут равны, а значит, окружность разделена на пять равных частей. После этого можно поделить круг. Для этого из точки О проведите отрезки к точкам, делящим окружность. В результате получится пять секторов одинаковой площади, которые делят круг на равные части.
3
Чтобы разделить круг на пять равных частей, используйте транспортир. Проведите радиус окружности и от центра и этого радиуса отложите угол 36º. Угол опишет сектор, площадь которого будет равна 1/5 площади окружности. Проделайте эту операцию еще три раза, получив пять равных секторов, которые и поделят круг на пять равных частей.
Источники:
- как разделить окружность на 5 равных частей