Инструкция
1
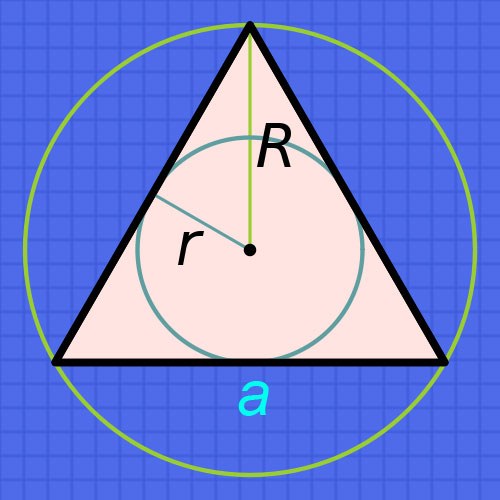
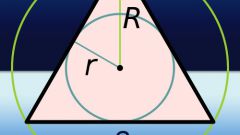
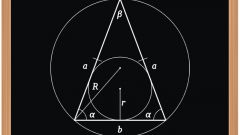
Если известен радиус окружности (r), вписанной в правильный треугольник, то для нахождения длин его сторон (a), увеличьте радиус в шесть раз и разделите результат на квадратный корень из тройки: a=r•6/√3. Например, если этот радиус равен 15 сантиметрам, то длина каждой стороны приблизительно будет равна 15•6/√3≈90/1,73≈52,02 сантиметрам.
2
Если известен радиус не вписанной, а описанной возле такого треугольника окружности (R), то исходите из того, что радиус описанной окружности всегда вдвое больше радиуса вписанной. Из этого вытекает, что формула расчета длины стороны (a) будет почти совпадать с описанной на предыдущем шаге - увеличьте известный радиус только в три раза, а результат разделите на квадратный корень из тройки: a=R•3/√3. Например, если радиус такой окружности равен 15 сантиметрам, то длина каждой стороны приблизительно будет равна 15•3/√3≈45/1,73≈26,01 сантиметрам.
3
Если известна высота (h), проведенная из любой вершины правильного треугольника, то для нахождения длины каждой его стороны (a) находите частное от деления удвоенной высоты на квадратный корень из тройки: a=h•2/√3. Например, если высота составляет 15 сантиметров, то длины сторон будут равны 15•2/√3≈60/1,73≈34,68 сантиметра.
4
Если известна длина периметра правильного треугольника (P), то для нахождения длин сторон (a) этой геометрической фигуры просто уменьшите его втрое: a=P/3. Например, если периметр составляет 150 сантиметров, то длина каждой из сторон будет равна 150/3=50 сантиметрам.
5
Если известна только площадь такого треугольника (S), то для нахождения длины каждой его стороны (a) посчитайте квадратный корень из частного от деления учетверенной площади на квадратный корень из тройки: a=√(4•S/√3). Например, если площадь равна 150 квадратным сантиметрам, то длина каждой стороны приблизительно будет равна √(4•150/√3)≈√(600/1,73)≈18,62 сантиметрам.
Источники:
- сторона правильного треугольника