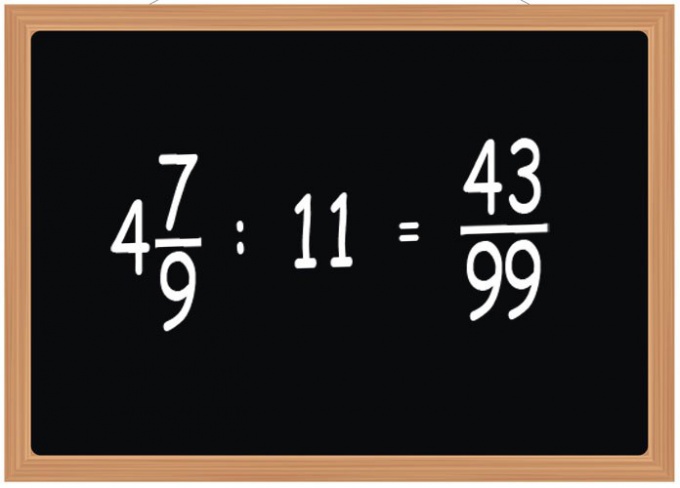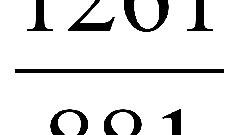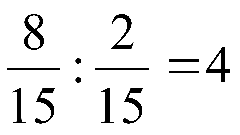Как разделить дробь на натуральное число

Если число может быть использовано при счете каких-нибудь предметов, то его можно считать «натуральным», то есть натуральными являются все целые неотрицательные числа. А дробным называют число, в числителе и знаменателе которого стоят натуральные числа. Существует несколько форм записи дробного числа, для каждой из которых операция деления на натуральное число имеет индивидуальные особенности.

Инструкция

1. Если дробное число не записано в смешанной форме, то пропустите этот шаг, а иначе для того, чтобы разделить его на натуральное число, сначала приведите смешанную дробь к неправильной форме записи обыкновенной дроби. В смешанной форме целая часть пишется перед дробной - вам надо умножить ее на число, стоящее в знаменателе, и прибавить полученный результат к числителю. Например, смешанную дробь 4 7/9 надо записать в виде 43/9, так как 4*9+7=36+7=43. Знаменатель дробной части при этом преобразовании остается без изменений, а полученная дробь называется «неправильной», так как он меньше рассчитанного числителя.
2. Если число, стоящее в числителе обыкновенной дроби можно без остатка разделить на натуральное число, данное в условиях задачи, то все процедура сведется к одной только этой операции. Например, чтобы разделить неправильную дробь 44/9 на натуральное число 11 достаточно разделить на него числитель, оставив знаменатель без изменений 44/9 : 11 = 4/9.
3. Если же число, стоящее в числителе обыкновенной дроби не делится без остатка на данное натуральное число, то умножьте на это число знаменатель обыкновенной дроби, а числитель оставьте без изменений. Например, чтобы полученную на первом шаге неправильную обыкновенную дробь 43/9 разделить на натуральное число 11, надо в числителе оставить 43, а в знаменатель поставить результат умножения 9*11=99, то есть результатом будет 43/99.
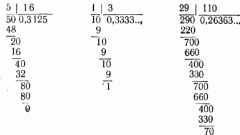
4. Если дробь, которую требуется поделить, записана в десятичной форме, то, как правило, представлять результат требуется тоже в форме десятичной дроби. Поэтому вам просто следует поделить любым удобным способом (в столбик, в уме или с помощью калькулятора) дробь на данное число. Например, результатом деления десятичной дроби 3,14 на натурально число 2 будет десятичная дробь 1,57.
5. Если все же требуется представить результат деления десятичной дроби на натуральное число в форме обыкновенной дроби, то начните с приведения десятичной формы записи к смешанной обыкновенной форме. Для этого поставьте в числитель десятичную дробь, убрав из нее запятую. В знаменатель поставьте единицу, затем посчитайте количество знаков в дробной части исходной десятичной дроби и припишите к единице такое же количество нулей. Например, десятичная дробь 3,14 будет выглядеть в формате обыкновенной дроби как 314/100. После этого действуйте так же, как описано выше, начиная со второго шага.