Как определить диаметр круга

Отрезок, соединяющий две несовпадающие точки, лежащие на одной окружности, называют «хордой», а хорда, проходящая через центр этой окружности, имеет и еще одно название - «диаметр». Такая хорда имеет максимально возможную для этой окружности длину, которую можно вычислить несколькими способами, используя базовые определения и соотношения.

Инструкция

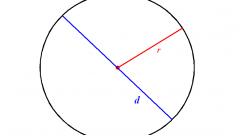
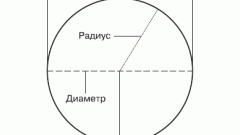
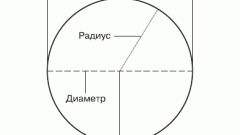
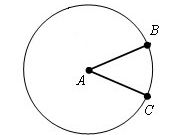
1. Самый простой способ определения диаметра (D) окружности можно применять в том случае, когда известен радиус (R) круга. По определению радиус - это отрезок, соединяющий центр круга с любой точкой, лежащей на окружности. Из этого вытекает, что диаметр составляют два отрезка, длина каждого из которых равна радиусу: D=2*R.
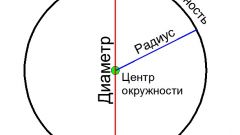
2. Используйте для вычисления диаметра (D) соотношение, называемое числом Пи, если вам известна длина периметра (L). Периметр, применительно к кругу, принято называть длиной окружности, а число Пи выражает постоянное соотношение между диаметром и длиной окружности - в евклидовой геометрии деление периметра круга на его диаметр всегда равно числу Пи. Значит, для нахождения диаметра длину окружности вам нужно разделить на эту константу: D=L/π.
3. Из корень из результата деления площади на число Пи и удвоить полученное значение: D=2*√(S/π).
4. Если возле круга описан прямоугольник и длина его стороны известна, то ничего вычислять не потребуется - таким прямоугольником может быть только квадрат, а длина его стороны будет равна диаметру круга.
5. В случае же вписанного в круг прямоугольника длина диаметра будет совпадать с длиной его диагонали. Для ее нахождения при известных ширине (H) и высоте (V) прямоугольника можно воспользоваться теоремой Пифагора, так как треугольник, образованный диагональю, шириной и высотой будет прямоугольным. Из теоремы вытекает, что длина диагонали прямоугольника, а значит и диаметра окружности, равна квадратному корню из суммы квадратов ширины и высоты: D= √(H²+V²).