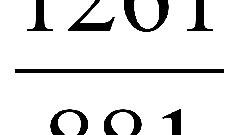Инструкция
1
Для сокращения обыкновенной дроби надо ее числитель и знаменатель разделить на их наибольший общий множитель. На практике обычно сокращение дроби производят в несколько этапов. Для численных дробей "на глазок" прикидывают, на какое число можно разделить и числитель, и знаменатель. Затем делят на это число, а потом снова пытаются сократить полученную дробь до тех пор, пока у числителя и знаменателя есть общие множители.
Из этого вытекает простейший способ сокращения дроби - разложение числителя и знаменателя на простые сомножители. Если сходу обнаружить хоть один общий множитель не удается, то начинают перебирать простые числа и выяснять, есть ли среди них такое, на которое делятся числитель и знаменатель дроби.
Из этого вытекает простейший способ сокращения дроби - разложение числителя и знаменателя на простые сомножители. Если сходу обнаружить хоть один общий множитель не удается, то начинают перебирать простые числа и выяснять, есть ли среди них такое, на которое делятся числитель и знаменатель дроби.
2
В том случае когда дробь представлена в виде частного многочленов, многочлены надо разложить на множители, пользуясь формулами сокращенного умножения или другими способами пытаясь привести их в форму произведения одночленов. Обычно умение правильно и быстро подобрать формулу сокращенного умножения приходит только с опытом.
Обратите внимание
Для сокращения дробей неважно, является ли дробь правильной или неправильной, главное, чтобы она была представлена в виде числителя и знаменателя.
Полезный совет
Воспользуйтесь признаками делимости на разные числа, стараясь найти наибольший общий множитель числителя и знаменателя.
Если числитель представлен в форме произведения одночленов, а знаменатель нет (и наоборот), попробуйте поделить многочлен знаменателя поочередно на одночлены числителя. Возможно, один из них окажется множителем и для знаменателя.
Если числитель представлен в форме произведения одночленов, а знаменатель нет (и наоборот), попробуйте поделить многочлен знаменателя поочередно на одночлены числителя. Возможно, один из них окажется множителем и для знаменателя.
Источники:
- как сократить правильную дробь