Инструкция
1
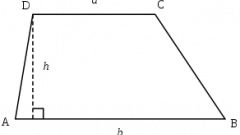
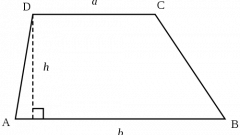
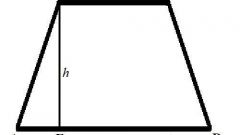
Начертите прямоугольную трапецию ABCD. Боковые стороны этой фигуры обозначьте, соответственно, как AB и DC. Первая боковая сторона DC совпадает с высотой трапеции. Она перпендикулярна двум основаниям прямоугольной трапеции.
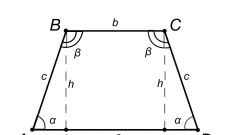
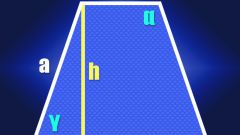
Существует несколько способов нахождения боковых сторон. Так например, если в задаче дана вторая боковая сторона BA и угол ABH=60, то первую высоту найдите наиболее простым из способов, проведя высоту BH:
BH=AB*sinα
Поскольку BH=CD, то СD=AB*sinα=√3AB/2
Существует несколько способов нахождения боковых сторон. Так например, если в задаче дана вторая боковая сторона BA и угол ABH=60, то первую высоту найдите наиболее простым из способов, проведя высоту BH:
BH=AB*sinα
Поскольку BH=CD, то СD=AB*sinα=√3AB/2
2
3
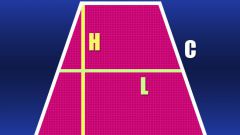
Задачу можно решить и в том случае, если значения углов неизвестны, при условии, что даны два основания и боковая сторона AB. Однако, в этом случае можно найти только сторону CD, которая является высотой трапеции. Первоначально, зная значения оснований, найдите длину отрезка AH. Он равен разности большего и меньшего оснований, поскольку известно, что BH=CD:
AH=AD-BC
Затем, используя теорему Пифагора, найдите высоту BH, равную стороне CD:
BH=√AB^2-AH^2
AH=AD-BC
Затем, используя теорему Пифагора, найдите высоту BH, равную стороне CD:
BH=√AB^2-AH^2
4
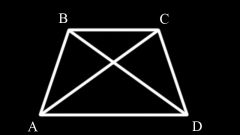
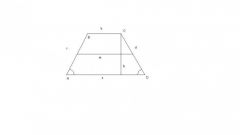
Если у прямоугольной трапеции есть диагональ BD и угол 2α, как показано на рисунке 2, то сторону AB можно найти также по теореме Пифагора. Для этого, сначала вычислите длину основания AD:
AD=BD*cos2α
Затем найдите сторону AB следующим образом:
AB=√BD^2-AD^2
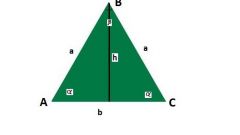
После этого докажите подобие треугольников ABD и BCD. Так как у этих треугольников одна общая сторона - диагональ, и при этом, два угла равны, как видно из рисунка, то эти фигуры подобны. На основании этого доказательства найдите вторую боковую сторону. Если известно верхнее основание и диагональ, то сторону найдите обычным образом с использованием стандартной теоремы косинусов:
c^2=а^2+b^2-2ab cos α, где а, b, с - стороны треугольника, α - угол между сторонами а и b.
AD=BD*cos2α
Затем найдите сторону AB следующим образом:
AB=√BD^2-AD^2
После этого докажите подобие треугольников ABD и BCD. Так как у этих треугольников одна общая сторона - диагональ, и при этом, два угла равны, как видно из рисунка, то эти фигуры подобны. На основании этого доказательства найдите вторую боковую сторону. Если известно верхнее основание и диагональ, то сторону найдите обычным образом с использованием стандартной теоремы косинусов:
c^2=а^2+b^2-2ab cos α, где а, b, с - стороны треугольника, α - угол между сторонами а и b.