Как найти наклонную асимптоту

Асимптота функции — линия, к которой неограниченно приближается график этой функции. В широком смысле асимптотическая линия может быть и криволинейной, однако чаще всего этим словом обозначают прямые линии.

Инструкция

1. Если заданная функция имеет асимптоты, то они могут быть вертикальными или наклонными. Существуют также горизонтальные асимптоты, являющиеся частным случаем наклонных.
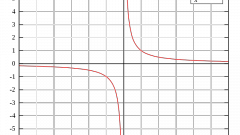
2. Предположим, что вам дана функция f(x). Если она не определена в некоторой точке x0 и по мере приближения x к x0 слева или справа f(x) стремится к бесконечности, то в этой точке функция имеет вертикальную асимптоту. Например, в точке x = 0 лишаются смысла функции 1/x и ln(x). Если x → 0, то 1/x → ∞, а ln(x) → -∞. Следовательно, обе функции в этой точке имеют вертикальную асимптоту.
3. Наклонная асимптота — прямая, к которой неограниченно стремится график функции f(x) по мере того, как x неограниченно возрастает или убывает. Функция может иметь и вертикальные, и наклонные асимптоты.
   
   В практических целях различают наклонные асимптоты при x → ∞ и при x → -∞. В ряде случаев функция может стремиться к одной и той же асимптоте в обе стороны, но, вообще говоря, они не обязаны совпадать.
4. Асимптота, как и всякая наклонная прямая, имеет уравнение вида y = kx + b, где k и b — константы.
   
   Прямая будет наклонной асимптотой функции при x → ∞, если по мере стремления x к бесконечности разность f(x) - (kx+b) стремится к нулю. Аналогично, если эта разность стремится к нулю при x → -∞, то прямая kx + b будет наклонной асимптотой функции в этом направлении.
5. Чтобы понять, имеет ли заданная функция наклонную асимптоту, и если имеет — найти ее уравнение, нужно вычислить константы k и b. Метод вычисления не меняется от того, в каком направлении вы ищете асимптоту.
   
   Константа k, также называемая угловым коэффициентом наклонной асимптоты, является пределом отношения f(x)/x при x → ∞.
   
   Например, путь задана функция f(x) = 1/x + x. Отношение f(x)/x будет в этом случае равно 1 + 1/(x^2). Его предел при x → ∞ равен 1. Следовательно, заданная функция имеет наклонную асимптоту с угловым коэффициентом 1.
   
   Если коэффициент k получается нулевым, это значит, что наклонная асимптота заданной функции горизонтальна, и ее уравнение y = b.
6. Чтобы найти константу b, то есть смещение нужной нам прямой, понадобится вычислить предел разности f(x) - kx. В нашем случае эта разность равна (1/x + x) - x = 1/x. При x → ∞ предел 1/x равен нулю. Таким образом, b = 0.
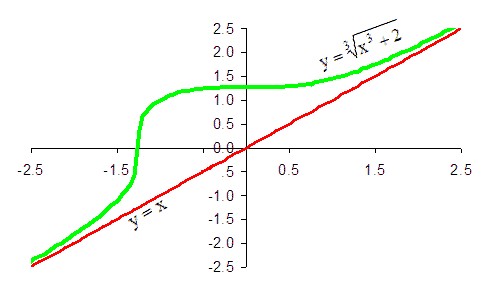
7. Окончательный вывод состоит в том, что функция 1/x + x имеет наклонную асимптоту в направлении плюс бесконечности, уравнение которой y = x. Тем же способом легко доказать, что эта же прямая является наклонной асимптотой заданной функции и в направлении минус бесконечности.