Вам понадобится
- - лист бумаги;
- - ручка;
- - калькулятор;
- - призма с заданными параметрами;
- - теоремы синусов и косинусов в случае наклонной призмы.
Инструкция
1
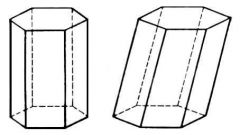
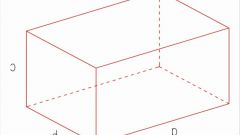
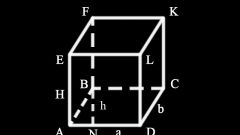
Постройте призму с заданными параметрами. Вам должны быть известны как минимум вид этого геометрического тела, размеры сторон основания, высота и угол наклона боковых ребер. Последнее условие необходимо для наклонной призмы.
2
Вычислите площадь боковой поверхности прямой призмы. Согласно определению, у данного геометрического тела боковые ребра перпендикулярны основанию. Это значит, что перпендикулярное сечение конгруэнтно обоим многоугольникам, лежащим в основании. То есть площадь боковой поверхности прямой призмы вычисляется умножением периметра основания на высоту. Это можно выразить формулой S=P*h, где P — периметр любого из оснований. Найдите его, сложив длины всех сторон. В некоторых случаях достаточно найти полупериметр и умножить его на 2.
3
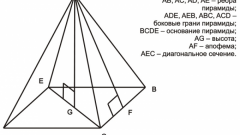
Чтобы найти полную площадь поверхности прямой призмы, приплюсуйте к полученной величине удвоенную площадь оснований. Если в основании лежит треугольник или четырехугольник, стороны которого вам известны, площадь высчитывается по обычной формуле для данной геометрической фигуры. Но многоугольник может быть и более сложным. В этом случае сделайте дополнительные построения, расчленив его на фигуры с известными вам параметрами или теми, которые можно достаточно легко найти.
4
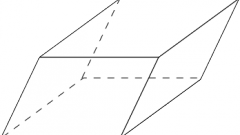
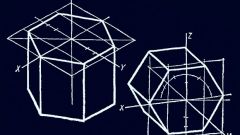
Для вычисления площади боковой поверхности наклонной призмы необходимо построить перпендикулярное сечение. Это такое сечение, которое перпендикулярно всем ребрам. Его можно расположить так, чтобы оно отсекало от некоторых граней треугольник, образованный ребром между основанием и боковой гранью, частью бокового ребра и линией перпендикулярного сечения. Если основание являет собой неправильный многоугольник, линии бокового сечения, принадлежащие разным граням, придется вычислять отдельно. Это можно сделать по теоремам синусов и косинусов, используя заданные углы наклона.
5
Вычислив стороны перпендикулярного сечения, сложите их длины и получите периметр. Умножив его на заданную высоту, вы получите площадь боковой поверхности наклонной призмы. S=P'*h. P' в данном случае означает периметр перпендикулярного сечения.
Источники:
- площадь полной поверхности призмы формула