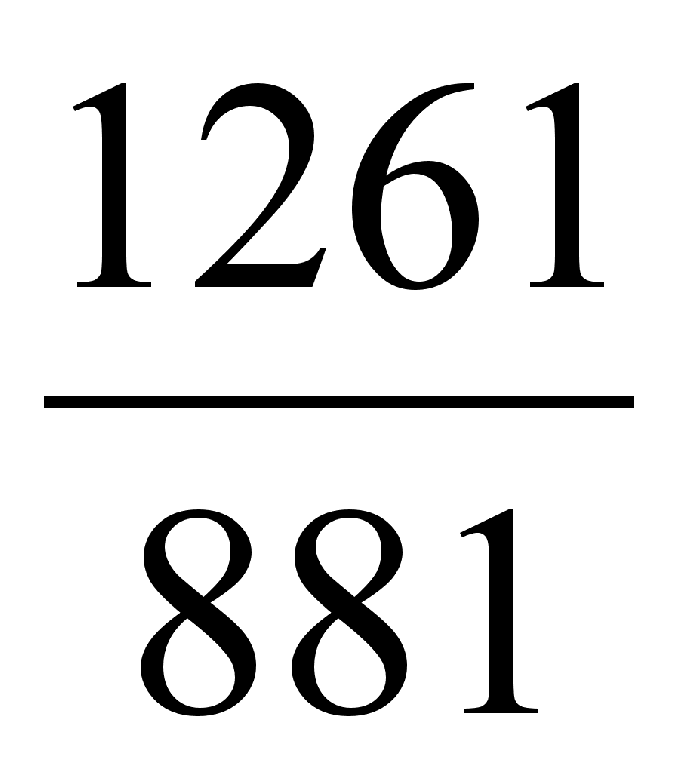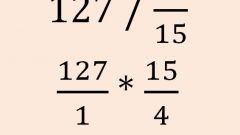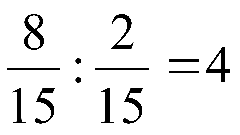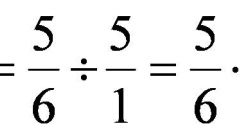Вам понадобится
- - лист бумаги;
- - ручка;
- - калькулятор.
Инструкция
1
Перемножьте правильную (записанную, как отношение числителя к знаменателю) дробь и натуральное число: числитель дроби, или делимое, умножьте на число и результат запишите в числитель (число, которое расположено над горизонтальной чертой – разделителем дроби). Знаменатель (делитель) остается прежним.
2
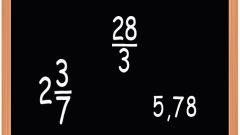
Перемножьте смешанную (записанную, как правильная дробь и целое число) дробь и натуральное число: умножьте целую часть и числитель дроби на это число, а знаменатель оставьте без изменений. Смешанная дробь является суммой целой дроби и числа.
3
Перемножьте две дроби между собой: сначала перемножьте между собой числители дробей, и запишите результат в числитель, а потом, соответственно, перемножьте знаменатели и результат запишите в знаменатель.
4
Перемножьте между собой смешанные дроби: вначале запишите дроби в виде неправильных, в которых модуль числителя больше модуля знаменателя. Для этого умножьте на знаменатель целую часть дроби и прибавьте полученное произведение к числу в числителе. После преобразования перемножьте, соответственно, числители и знаменатели дробей и запишите результат в виде неправильной дроби.
5
Разделите одну дробь на другую: поменяйте местами числитель и знаменатель во второй дроби – получите обратную дробь и умножьте полученную дробь на первую так, как описано выше.
Обратите внимание
Помните, что деление на ноль не производится, поскольку результатом в таком случае будет математическая неопределенность.
Полезный совет
Сокращайте дроби при расчетах до наименьшего значения – это позволит быстрее произвести вычисление и получить результат. Получите окончательный ответ, разделив, если это возможно, и числитель, и знаменатель дроби на наибольший общий делитель.