Инструкция
1
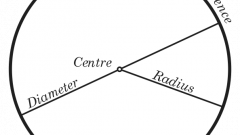
Знайте, что кривыми можно описать движение жидкости, газа, световых лучей, линий тока. Радиусом кривизны для плоской кривой в определенной точке является радиус касательной окружности в этой точке. В некоторых случаях кривая задается уравнениями, и радиус кривизны вычисляется по формулам. Соответственно, чтобы узнать радиус кривизны, необходимо узнать радиус окружности, касающейся определенной точки.
2
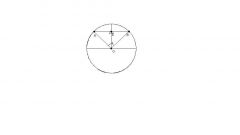
Определите на плоскости кривой точку А, вблизи нее возьмите еще одну точку В. Постройте касательные к имеющейся кривой, которые проходят через точки А и В.
3
Проведите через точки А и В линии, перпендикулярные построенным касательным, продлите их до пересечения. Обозначьте точку пересечения перпендикуляров, как О. Точка О является центром касательной окружности в данной точке. Значит ОА – радиус окружности, т.е. кривизны в данной конкретной точке А.
4
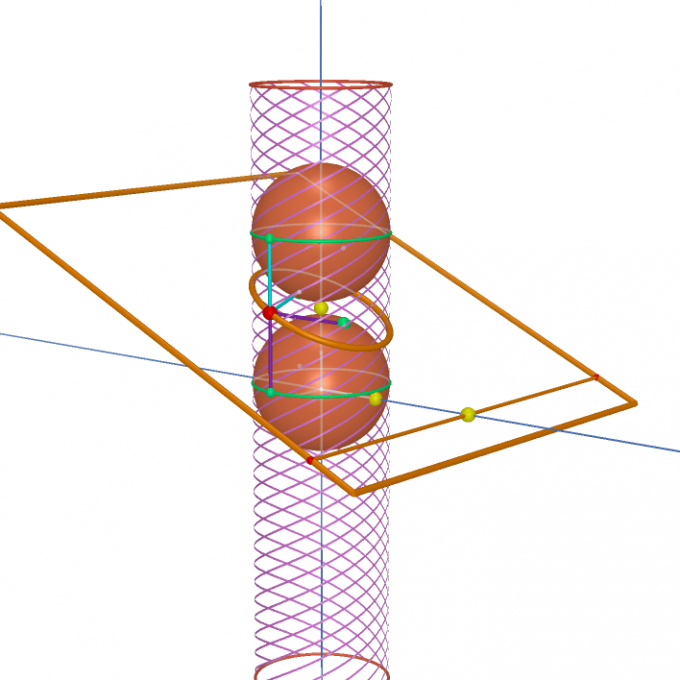
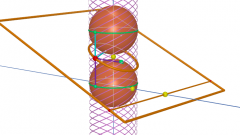
Заметим, что при движении точки по любой криволинейной траектории в любой момент движения она движется по какой-то окружности, которая меняется от точки к точке.
5
Если для точки в пространстве определить кривизны в двух взаимно перпендикулярных направлениях, то эти кривизны будут называться главными. Направление главных кривизн должно быть обязательно 900. Для вычислений часто используют среднюю кривизну, равную полусумме главных кривизн, и гауссову кривизну, равную их произведению. Существует также понятие кривизны кривой. Это величина, обратная радиусу кривизны.
6
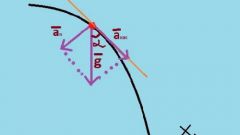
Ускорение является важным фактором движения точки. Кривизна траектории напрямую влияет на ускорение. Ускорение возникает в том случае, когда точка с постоянной скоростью начинает двигаться по кривой. Меняется не только абсолютная величина скорости, но и ее направление, возникает центростремительное ускорение. Т.е. в реальности точка начинает двигаться по окружности, которой касается в данный момент времени.