Инструкция
1
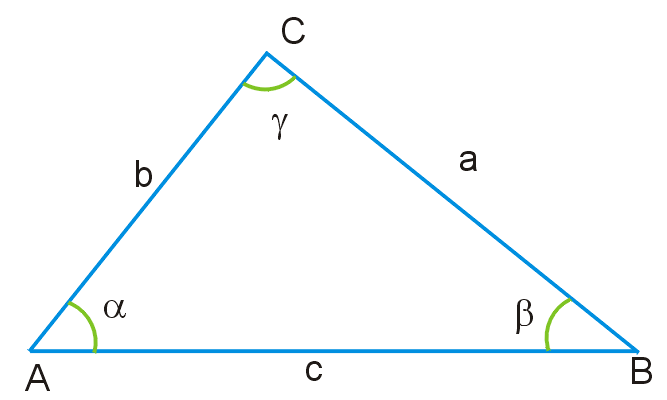
Представьте себе, что дан треугольник, у которого известны длины двух сторон и значение одного угла. Все углы этого треугольника не равны друг другу, а его стороны также являются различными по величине. Угол γ лежит напротив стороны треугольника, обозначенной, как AB, которая является основанием этой фигуры. Через данный угол, а также через оставшиеся стороны AC и BC можно найти ту сторону треугольника, которая неизвестна, по теореме косинусов, выведя на ее основе представленную ниже формулу:
a^2=b^2+c^2-2bc*cosγ, где a=BC, b=AB, c=AC
Теорему косинусов иначе называют обобщенной теоремой Пифагора.
2
Теперь представьте себе, что даны все три стороны фигуры, но при этом ее угол γ неизвестен. Зная, что формула имеет вид a^2=b^2+c^2-2bc*cosγ, преобразуйте данное выражение таким образом, чтобы искомой величиной стал угол γ: b^2+c^2=2bc*cosγ+a^2.
Затем приведите показанное выше уравнение к несколько иному виду: b^2+c^2-a^2=2bc*cosγ.
Затем данное выражение следует преобразовать в представленное ниже: cosγ=√b^2+c^2-a^2/2bc.
Осталось подставить в формулу числа и осуществить вычисления.
3
Чтобы найти косинус угла треугольника, обозначенного как γ, его необходимо выразить через обратную тригонометрическую функцию, называемую арккосинусом. Арккосинусом числа m называется такое значение угла γ, для которого косинус угла γ равен m. Функция y=arccos m является убывающей. Представьте себе, например, что косинус угла γ равен одной второй. Тогда угол γ может быть определен через арккосинус следующим образом:
γ = arccos, m = arccos 1/2 = 60°, где m = 1/2.
Аналогичным образом можно найти и остальные углы треугольника при двух других неизвестных его сторонах.
4
В случае, если углы представлены в радианах, переведите их в градусы, используя следующее соотношение:
π радиан = 180 градусов.
Помните, что подавляющее большинство инженерных калькуляторов снабжено возможностью переключения единиц измерения углов.