Вам понадобится
- калькулятор
Инструкция
1
ля начала вам следует определиться с понятием медианы (узнать, что она означает).
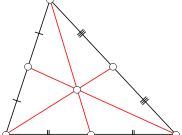
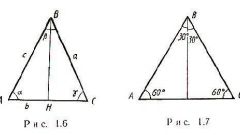
Посмотрите на произвольный треугольник АВС. ВD-отрезок, который соединяет вершину треугольника с серединой противоположной стороны, и есть медиана.
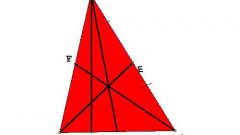
Таким образом, благодаря вышеизложенному определению и сопровождающему его рисунку 1 вам должно быть понятно, что любой треугольник имеет 3 медианы, которые пересекаются внутри этой фигуры.
Точка пересечения медиан является центром тяжести треугольника, или, как его еще называют, центром масс. Каждая медиана делится точкой пересечения медиан в отношении 2:1, считая от вершины.
Обратите внимание еще на тот факт, что треугольники, на которые будет разбит исходный треугольник, всеми своими медианами имеют одинаковые площади.
Посмотрите на произвольный треугольник АВС. ВD-отрезок, который соединяет вершину треугольника с серединой противоположной стороны, и есть медиана.
Таким образом, благодаря вышеизложенному определению и сопровождающему его рисунку 1 вам должно быть понятно, что любой треугольник имеет 3 медианы, которые пересекаются внутри этой фигуры.
Точка пересечения медиан является центром тяжести треугольника, или, как его еще называют, центром масс. Каждая медиана делится точкой пересечения медиан в отношении 2:1, считая от вершины.
Обратите внимание еще на тот факт, что треугольники, на которые будет разбит исходный треугольник, всеми своими медианами имеют одинаковые площади.
2
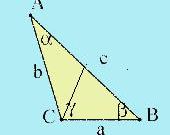
Для того, чтобы рассчитать медиану, вам необходимо воспользоваться специально разработанным алгоритмом. Формула для расчета медианы через рисунке 2,
где m(a) - медиана треугольника АВС, соединяющая вершину A с серединой стороны BС,
b – сторона АС треугольника АВС,
с – сторона АВ треугольника АВС,
а – сторона ВС треугольника АВС.
Из представленной формулы следует, что зная длины всех медиан треугольника, вы сможете найти длину любой его стороны.
где m(a) - медиана треугольника АВС, соединяющая вершину A с серединой стороны BС,
b – сторона АС треугольника АВС,
с – сторона АВ треугольника АВС,
а – сторона ВС треугольника АВС.
Из представленной формулы следует, что зная длины всех медиан треугольника, вы сможете найти длину любой его стороны.
3
Если вам нужна формула для нахождения стороны треугольника через его медианы, то она выглядит, как показано на рисунке 3, где:
a – сторона ВС треугольника АВС,
m(b) - медиана, выходящая из вершины В,
m(c)- медиана, выходящая из вершины С,
m(a) –медиана, выходящая из вершины А.
a – сторона ВС треугольника АВС,
m(b) - медиана, выходящая из вершины В,
m(c)- медиана, выходящая из вершины С,
m(a) –медиана, выходящая из вершины А.
4
Для правильного расчета медианы вам необходимо ознакомится и с частными случаями, которые могут встречаться при решении уравнений с присутствием в них произвольного треугольника.
1. В равностороннем треугольнике, медиана, выходящая из вершины, которую образуют равные стороны, является:
- биссектрисой угла, образованного равными сторонами треугольника;
-высотой данного треугольника;
2. В равностороннем треугольнике все медианы равны. Все медианы являются биссектрисами соответствующих углов и высотами данного треугольника.
1. В равностороннем треугольнике, медиана, выходящая из вершины, которую образуют равные стороны, является:
- биссектрисой угла, образованного равными сторонами треугольника;
-высотой данного треугольника;
2. В равностороннем треугольнике все медианы равны. Все медианы являются биссектрисами соответствующих углов и высотами данного треугольника.
Видео по теме
Источники:
- как рассчитать медиану ряда