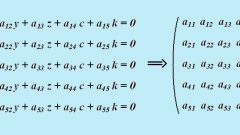Инструкция
1
Матрица называется ступенчатой, если выполнены следующие условия:
• после нулевой строки идут только нулевые строки;
• первый ненулевой элемент в каждой последующей строке расположен правее, чем в предыдущей.
В линейной алгебре имеется теорема, согласно которой любая матрица может быть приведена к ступенчатому виду путем следующих элементарных преобразований:
• перемена местами двух строк матрицы;
• прибавление к одной строке матрицы другой её строки, умноженной на число.
• после нулевой строки идут только нулевые строки;
• первый ненулевой элемент в каждой последующей строке расположен правее, чем в предыдущей.
В линейной алгебре имеется теорема, согласно которой любая матрица может быть приведена к ступенчатому виду путем следующих элементарных преобразований:
• перемена местами двух строк матрицы;
• прибавление к одной строке матрицы другой её строки, умноженной на число.
2
Рассмотрим приведение матрицы к ступенчатому виду на примере матрицы A, представленной на рисунке. Решая задачу, первым делом внимательно изучите строки матрицы. Возможно ли переставить местами строчки так, чтобы в дальнейшем было удобнее проводить вычисления. В нашем случае мы видим, что будет удобно поменять местами первую и вторую строчки. Во-первых, если первый элемент первой строчки равен числу 1, то это значительно упрощает последующие элементарные преобразования. Во-вторых, вторая строчка уже будет соответствовать ступенчатому виду, т.е. первый её элемент равен 0.
3
Далее обнулите все первые элементы столбцов (кроме первой строки). В нашем случае это сделать проще, т.к. первая строка начинается с числа 1. Поэтому мы последовательно умножаем первую строчку на соответствующее число и вычитаем из получившейся строки строчку матрицы. Обнуляя третью строку, умножаем первую строчку на число 5 и вычитаем из результата третью строку. Обнуляя четвертую строку, умножаем первую строку на число 2 и вычитаем из результата четвертую строку.
4
Следующим этапом обнулите вторые элементы строк, начиная с третьей строки. Для нашего примера для обнуления второго элемента третьей строчки достаточно умножить вторую строчку на число 6 и вычесть из результата третью строчку. Для получения нуля в четвертой строчке придется выполнить более сложное преобразование. Надо умножить вторую строчку на число 7, а четвертую строчку на число 3. Таким образом мы получим на месте второго элемента строк число 21. Далее вычитаем одну строчку из другой и получаем на месте второго элемента 0.
5
И наконец, обнуляем третий элемент четвертой строки. Для этого необходимо умножить третью строку на число 5, а четвертую строку на число 3. Вычитаем одну строку из другой и получаем матрицу A, приведенную к ступенчатому виду.
Обратите внимание
Если числа строк небольшие или удобные для проведения вычислений, то можно выполнять сразу несколько операций за один шаг. В других случаях лучше не торопиться и записать каждый шаг в отдельности.
Полезный совет
В интернете можно найти программы, приводящие матрицу к ступенчатому виду. Их очень удобно использовать для проверки получившегося результата.