Инструкция
1
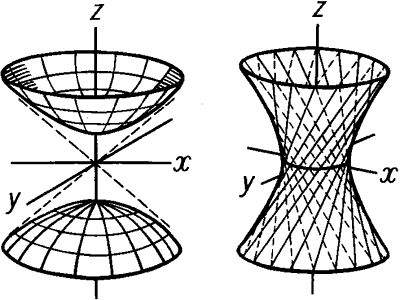
Представьте, что имеется гипербола и некоторая линия, которая проходит через начало координат. Если гиперболу начать вращать вокруг этой оси, возникнет полое тело вращения, которое называется гиперболоидом. Существует два вида гиперболоидов: однополостный и двуполостный. Однополостный гиперболоид задается уравнением вида:x^2/a^2 +y^2/b^2-z^2/c^2=1Если рассматривать данную пространственную фигуру относительно плоскостей Oxz и Oyz, можно заметить, что основными ее сечениями являются гиперболы. Однако, сечением однополостного гиперболоида плоскостью Oxy является эллипс. Самый маленький эллипс гиперболоида называется горловым эллипсом. В этом случае, z=0, а эллипс проходит через начало координат. Уравнение горлового эллипса при z=0 записывается следующим образом:x^2/a^2 +y^2/b^2=1Остальные эллипсы имеют уравнения следующего вида:x^2/a^2 +y^2/b^2=1+h^2/c^2, где h - высота однополостного гиперболоида.
2
Построение гиперболоида начните с изображения гиперболы в плоскости Xoz. Начартите действительную полуось, которая совпадает с осью y и мнимую полуось, совпадающую с z. Постройте гиперболу, а затем задайте некоторую высоту h гиперболоида. После этого, на уровне заданной высоты проведите прямые, параллельные Ox и пересекающие график гиперболы в нижних и верхних точках.Затем аналогичным образом в плоскости Oyz постройте гиперболу, где b - действительная полуось, проходящая через ось y, а с - мнимая полуось, также совпадающая с c.Постройте в плоскости Oxy параллелограмм, который получается путем соединения точек графиков гипербол. Начертите горловой эллипс таким образом, чтобы он был вписан в этот параллелограмм. Аналогичным образом постройте остальные эллипсы. В результате получится чертеж тела вращения - однополостного гиперболоида, изображенного на рис.1
3
Двуполостный гиперболоид получил свое название из-за двух разных поверхностей, которые образованы осью Oz. Уравнение такого гиперболоида имеет следующий вид:x^2/a^2 +y^2/b^2 -z^2/c^2=-1Две полости получаются при построении гиперболы в плоскости Oxz и Oyz. У двуполостного гиперболоида сечения - эллипсы:x^2/a^2-y^2/b^2=h^2/c^2-1Также, как и в случае с однополостным гиперболоидом, постройте в плоскостях Oxz и Oyz гиперболы, которые будут располагаться таким образом, как показано на рисунке 2. Постройте внизу и наверху параллелограммы для построения эллипсов. Построив эллипсы, уберите все проекции построения, а затем начертите двуполостный гиперболоид.