Инструкция
1
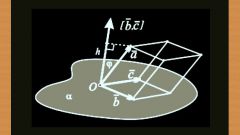
Пусть плоскость задана тремя принадлежащими ей точками K(xk;yk;zk), M(xm;ym;zm), P(xp;yp;zp). Чтобы найти нормальный вектор, составим уравнение этой плоскости. Обозначьте произвольную точку, лежащую на плоскости, буквой L, пусть у нее будут координаты (x;y;z). Теперь рассмотрите три вектора PK, PM и PL, они лежат на одной плоскости (компланарны), поэтому их смешанное произведение равно нулю.
2
Найдите координаты векторов PK, PM и PL:
PK = (xk-xp;yk-yp;zk-zp)
PM = (xm-xp;ym-yp;zm-zp)
PL = (x-xp;y-yp;z-zp)
Смешанное произведение этих векторов будет равно определителю, представленному на рисунке. Этот определитель следует вычислить, чтобы найти уравнение для плоскости. Вычисление смешанного произведения для конкретного случая смотрите в примере.
PK = (xk-xp;yk-yp;zk-zp)
PM = (xm-xp;ym-yp;zm-zp)
PL = (x-xp;y-yp;z-zp)
Смешанное произведение этих векторов будет равно определителю, представленному на рисунке. Этот определитель следует вычислить, чтобы найти уравнение для плоскости. Вычисление смешанного произведения для конкретного случая смотрите в примере.
3
Пример
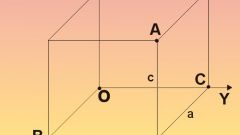
Пусть плоскость задана тремя точками K(2;1;-2), M(0;0;-1) и P(1;8;1). Требуется найти нормальный вектор плоскости.
Возьмите произвольную точку L с координатами (x;y;z). Вычислите векторы PK, PM и PL:
PK = (2-1;1-8;-2-1) = (1;-7;-3)
PM = (0-1;0-8;-1-1) = (-1;-8;-2)
PL = (x-1;y-8;z-1)
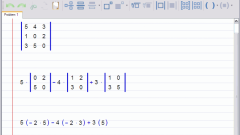
Составьте определитель для смешанного произведения векторов (он на рисунке).
Пусть плоскость задана тремя точками K(2;1;-2), M(0;0;-1) и P(1;8;1). Требуется найти нормальный вектор плоскости.
Возьмите произвольную точку L с координатами (x;y;z). Вычислите векторы PK, PM и PL:
PK = (2-1;1-8;-2-1) = (1;-7;-3)
PM = (0-1;0-8;-1-1) = (-1;-8;-2)
PL = (x-1;y-8;z-1)
Составьте определитель для смешанного произведения векторов (он на рисунке).
4
Теперь разложите определитель по первой строке, а затем подсчитайте значения определителей размера 2 на 2.
Таким образом уравнение плоскости -10x + 5y - 15z - 15 = 0 или, что то же, -2x + y - 3z - 3 = 0. Отсюда легко определить вектор нормали к плоскости: n = (-2;1;-3).
Таким образом уравнение плоскости -10x + 5y - 15z - 15 = 0 или, что то же, -2x + y - 3z - 3 = 0. Отсюда легко определить вектор нормали к плоскости: n = (-2;1;-3).
Источники:
- Уравнение плоскости, проходящей через три точки