Как найти катет прямоугольного треугольника, если известна гипотенуза

Треугольник – это часть плоскости, ограниченная тремя отрезками прямых, называемых сторонами треугольника, имеющими попарно по одному общему концу, называемых вершинами треугольника. Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным.

Инструкция

1. Стороны прямоугольного треугольника, прилегающие к прямому углу (AB и BC), называются катетами. Сторона, лежащая напротив прямого угла, называется гипотенузой (AC).
   
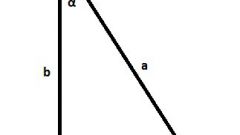
   Пусть нам известна гипотенуза AC прямоугольного треугольника ABC: |AC| = c. Обозначим угол с вершиной в точке A как ∟α, угол с вершиной в точке B как ∟β. Нам необходимо найти длины |AB| и |BC| катетов.
2. Пусть известен один из катетов прямоугольного треугольника. Предположим |BC| = b. Тогда мы можем воспользоваться теоремой Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2. Из данного уравнения находим неизвестный катет |AB| = a = √ (c^2 - b^2).
3. Пусть известен один из углов прямоугольного треугольника, предположим ∟α. Тогда катеты AB и BC прямоугольного треугольника ABC можно найти, используя тригонометрические функции. Так получаем: синус ∟α равен отношению противолежащего катета к гипотенузе sin α = b / c, косинус ∟α равен отношению прилежащего катета к гипотенузе cos α = a / c. Отсюда находим требуемые длины сторон: |AB| = a = с * cos α, |BC| = b = c * sin α.
4. Пусть известно соотношение катетов k = a / b. Также решаем задачу с использованием тригонометрических функций. Отношение a / b есть ни что иное, как котангенс ∟α: отношение прилежащего катета к противолежащему ctg α = a / b. В этом случае из данного равенства выражаем a = b * ctg α. И подставляем в теорему Пифагора a^2 + b^2 = c^2:
   
   b^2 * ctg^2 α + b^2 = c^2. Выносим b^2 за скобки, получаем b^2 * (ctg^2 α + 1) = c^2. И отсюда легко получаем длину катета b = c / √(ctg^2 α + 1) = c / √(k^2 + 1), где k – заданное соотношение катетов.
   
   По аналогии, если известно соотношение катетов b / a, решаем задачу с применением тригонометрической функции тангенс tg α = b / a. Подставляем значение b = a * tg α в теорему Пифагора a^2 * tg^2 α + a^2 = c^2. Отсюда a = c / √(tg^2 α + 1) = c / √(k^2 + 1), где k – заданное соотношение катетов.
5. Рассмотрим частные случаи.
   
   ∟α = 30°. Тогда |AB| = a = c * cos α = c * √3 / 2; |BC| = b = c * sin α = c / 2.
   
   ∟α = 45°. Тогда |AB| = |BC| = a = b = c * √2 / 2.