Инструкция
1
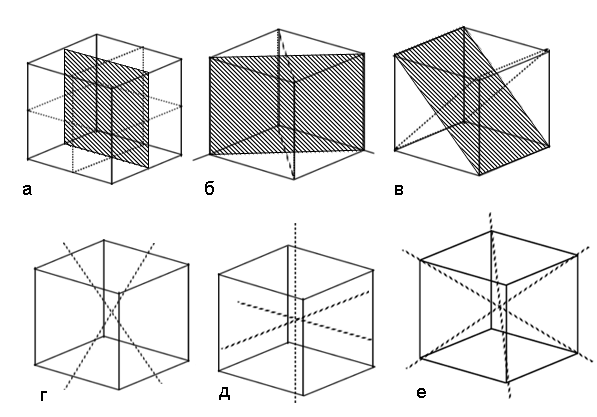
Диагональю называется любая прямая, соединяющая углы многогранников. Порядок ее нахождения зависит от вида фигуры (ромб, квадрат, параллелограмм) и от того, какие данные приведены в задаче. Наиболее простой способ нахождения диагонали прямоугольника состоит в следующем.Даны две стороны прямоугольника a и b. Зная, что все его углы равны 90°, а его диагональ является гипотенузой двух треугольников, можно сделать вывод, что диагональ этой фигуты можно найти по теореме Пифагора. В данном случае, стороны прямоугольника являются катетами треугольников. Отсюда следует, что диагональ прямоугольника равна:d=√(a^2+b^2)Частным случаем применения этого способа к нахождению диагонали является квадрат. Его диагональ также можно найти по теореме Пифагора, но, учитывая, что все его стороны равны, диагональ квадрата равна a√2. Величина a и есть сторона квадрата.
2
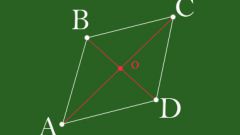
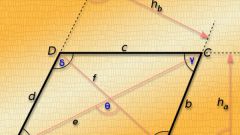
Если дан параллелограмм, то его диагональ находят, как правило, по теореме косинусов. Однако, в исключительных случаях при заданном значении второй диагонали можно найти первую из уравнения:d1=√2(a^2+b^2)-d2^2Теорема косинусов применима тогда, когда не дана вторая диагональ, а даны только стороны и углы. Она является обобщенной теоремой Пифагора. Допустим, дан параллелограмм, стороны которого равны b и c. Через два противоположных угла параллелограмма проходит диагональ a. Поскольку a, b и c образуют треугольник, можно применить теорему косинусов, по которой может быть вычислена диагональ:a^2=√b^2+c^2-2bc*cosα Когда дана площадь параллелограмма и одна из диагоналей, а также угол между двумя диагоналями, то диагональ можно вычислить следующим способом:d2=S/d1*cos
αРомбом называется параллелограмм, у которого все стороны равны. Пусть у него имеются две стороны, равные a, и, неизвестна диагональ. Тогда, зная теорему косинусов, диагональ можно вычислить по формуле:d=a^2+a^2-2a*a*cosα=2a^2(1-cosα)
3
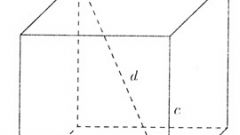
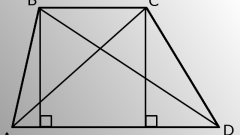
прямоугольной трапеции.Допустим, дана прямоугольная трапеция. Сначала нужно найти небольшой отрезок, который является катетом прямоугольного треугольника. Он равен разности верхнего и нижнего оснований. Поскольку трапеция прямоугольная, то из чертежа видно, что высота равна боковой стороне трапеции. Вследствие этого, можно найти другую боковую сторону трапеции. Если известны верхнее основание и боковая сторона, то по теореме косинусов может быть найдена первая диагональ:c^2=a^2+b^2-2ab*cosαВторая диагональ находится исходя из значений первой боковой стороны и верхнего основания по теореме Пифагора. В данном случае, эта диагональ является гипотенузой прямоугольного треугольника.