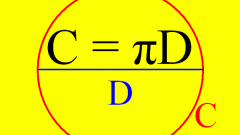Инструкция
1
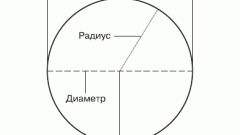
Длина окружности находится по формуле L=2πR, где R - радиус окружности. Таким образом, задача нахождения длины сводится к задаче нахождения радиуса окружности.
2
Рассмотрим правильный многоугольник с числом сторон, равным n. Пусть A - сторона этого n-угольника. В этом случае радиус описанной около него окружности равен R=A/2sin(π/n).Например, для правильного треугольника R=A/2sin(π/3), для правильного четырехугольника R=A/2sin(π/4), и т.д.
3
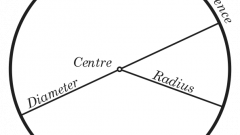
Теперь рассмотрим, как может быть найден радиус окружности, описанной около произвольного треугольника.1) Через длины сторон и площадь: R=abc/4S (a,b,c - стороны треугольника, S - площадь треугольника);2) Через сторону и величину угла, лежащего напротив стороны (следствие из теоремы синусов): R=A/2sin(a);К слову, если нам известны длины всех сторон треугольника, то его площадь можно найти по формуле Герона, и затем применить пункт 1.
Обратите внимание
Описать окружность около фигуры можно не всегда. Так, вокруг любого правильного многоугольника можно описать окружность. Так же, как и вокруг любого треугольника. Если вокруг выпуклого четырехугольника можно описать окружность, то сумма любой пары его противоположных углов равна π.