Инструкция
1
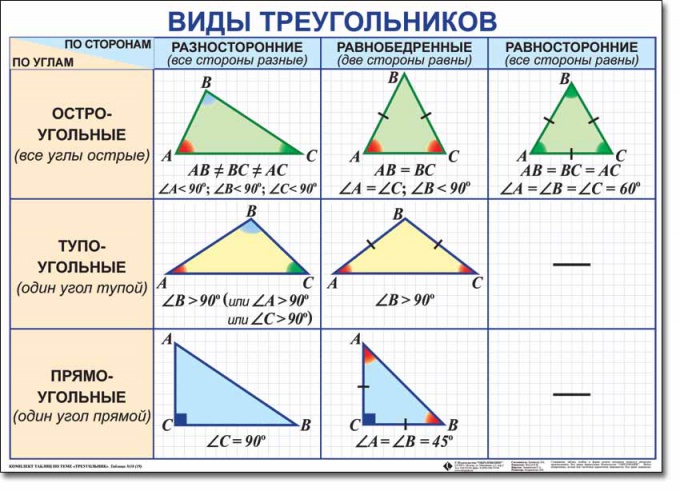
Принято выделять шесть видов треугольников. В основе этого деления лежат две классификации: по углам и по сторонам. Классификация по типам углов предполагает деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум видам. Например, он может быть прямоугольным и разносторонним одновременно.
2
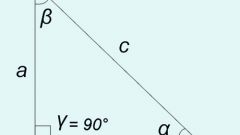
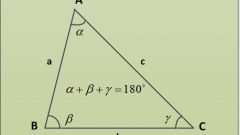
Определяя вид будьте очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является тупым, то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла являются острыми.
3
Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными. Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.
4
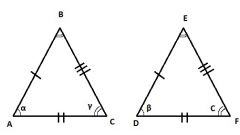
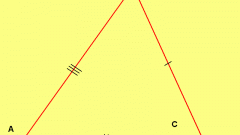
Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.
5
Равносторонним может быть назван только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.