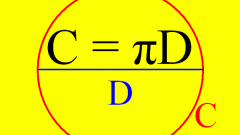Инструкция
1
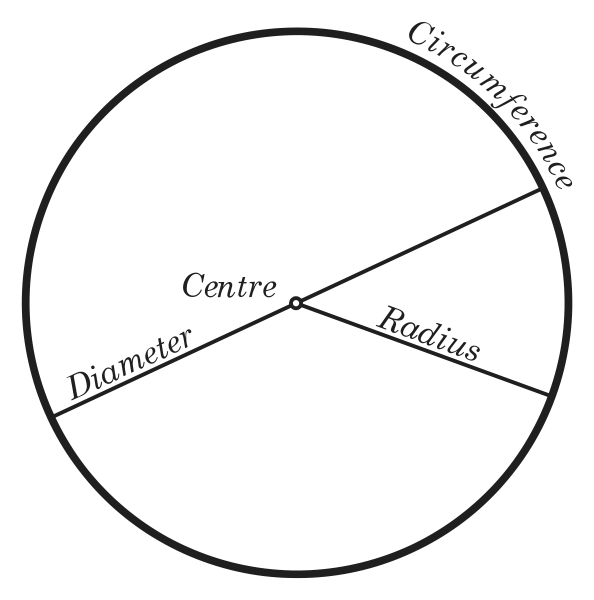
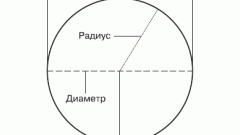
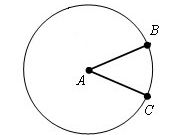
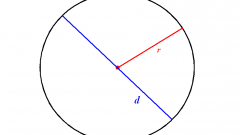
Окружность представляет собой кривую, ограничивающую плоскость, называемую кругом. Иными словами, окружностью называется геометрическое место точек плоскости, равноудаленных от ее центра. Отрезки соединенные с центром, окружности именуются ее радиусами, а расстояние от одной точки до другой, проходящее через центр, называется диаметром окружности. Диаметр окружности равен двум радиусам: D=2r. Уравнение окружности в аналитической геометрии имеет вид:x^2+y^2=R^2Существует также понятие хорды окружности. Она тоже получается путем соединения двух точек окружности, но не обязательно проходит через ее центр. Все диаметры, которые проходят через середину хорды, перпендикулярны ей. Самая большая хорда окружности является ее диаметром.
2
Как и любая кривая, окружность имеет некоторую длину p. Давно замечено, что длина окружности связана с ее диаметром числом π:p/d=πОтсюда следует, что p=πd, или p = 2πr, где r - радиус окружности.Число π имеет иррациональное значение, но приблизительно оно равно 3,14.Зная длину окружности, можно и определить площадь кольца, ограниченного двумя окружностями. Она равна:S=2πr*k, где k - расстояние между внутренней и внешней окружностями кольца; 2πr - длина внутренней окружности кольца.
3
Графический способ определения длины окружности, по причине его неточности, используют редко. Для этого используют курвиметр - прибор для измерения длины кривой линии. В любом месте окружности отмечают начальную точку измерения. К ней подносят курвиметр и ведут его по линии, пока снова не попадут в ту же точку.
4
приходится осуществлять физикам, астрономам. Первые вычисляют длину окружности элементарных частиц, вторые - небесных тел. Также, зная диаметр цирковой арены, беговой дорожки, руководствуясь приведенными выше формулами, можно вычислить, какое расстояние пробежит лошадь или бегун за один круг.