Вам понадобится
- Знания по геометрии.
Инструкция
1
Пусть дана сторона правильного треугольника с длиной a=7. Зная сторону такого треугольника можно легко вычислить его площадь. Для этого используется следующая формула: S = (3^(1/2)*a^2)/4. Подставим в это формулу значение а=7 и получим следующее: S = (7*7*3^1/2)/4 = 49 * 1,7 / 4 = 20,82. Таким образом получили, что площадь равностороннего треугольника со стороной а=7 равна S=20,82.
2
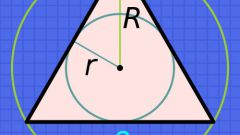
Если дан радиус вписанной в треугольник окружности, то формула площади через радиус будет выглядеть следующим образом:
S = 3*3^(1/2)*r^2, где r - радиус вписанной окружности. Пусть радиус вписанной окружности r=4. Подставим его в написанную ранее формулу и получим следующее выражение: S = 3*1,7*4*4 = 81,6. То есть при радиусе вписанной окружности равного 4 площадь равностороннего треугольника будет равна 81,6.
S = 3*3^(1/2)*r^2, где r - радиус вписанной окружности. Пусть радиус вписанной окружности r=4. Подставим его в написанную ранее формулу и получим следующее выражение: S = 3*1,7*4*4 = 81,6. То есть при радиусе вписанной окружности равного 4 площадь равностороннего треугольника будет равна 81,6.
3
При известном радиусе описанной окружности формула площади треугольника выглядит так: S = 3*3^(1/2)*R^2/4, где R - радиус описанной окружности. Допустим, что R=5, подставим это значение в формулу: S = 3*1,7*25/4 = 31,9. Получается, что при радиусе описанной окружности равного 5 площадь треугольника равна 31,9.
Обратите внимание
Площадь треугольника всегда величина положительная, также как и длина стороны треугольника и радиусы вписанной и описанной окружностей.
Полезный совет
Радиус вписанной и описанной окружности в равностороннем треугольнике отличается в два раза, зная это, можно запомнить только одну формулу, например через радиус вписанной окружности, а вторую выводить, зная это утверждение.