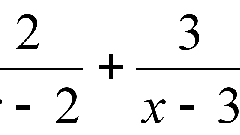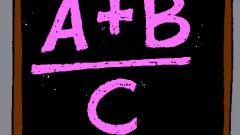Инструкция
1
Для начала можно рассмотреть простейший пример - 1/sqrt(2). Квадратный корень из двух - иррациональное число в знаменателе.В этом случае необходимо домножить числитель и знаменатель дроби на ее знаменатель. Это обеспечит рациональное число в знаменателе. Действительно, sqrt(2)*sqrt(2) = sqrt(4) = 2. Умножение двух одинаковых квадратных корней друг на друга даст в итоге то, что находится под каждым из корней: в данном случае - двойку.В итоге: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. Этот алгоритм подходит также к дробям, в знаменателе которых корень умножается на рациональное число. Числитель и знаменатель в этом случае нужно умножить на корень, находящийся в знаменателе.Пример: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = sqrt(3)/(2*3) = sqrt(3)/6.
2
Абсолютно аналогично нужно действовать, если в знаменателе находится не квадратный корень, а, скажем кубический или любой другой степени. Корень в знаменателе нужно умножать на точно такой же корень, на этот же корень умножать и числитель. Тогда корень перейдет в числитель.
3
В более сложном случае в знаменателе присутствует сумма или рационального числа или двух иррациональных чисел.В случае суммы (разности) двух квадратных корней или квадратного корня и рационального числа можно воспользоваться хорошо известной формулой (x+y)(x-y) = (x^2)-(y^2). Она поможет избавиться от иррациональности в знаменателе. Если в знаменателе разность, то домножать числитель и знаменатель нужно на сумму таких же чисел, если сумма - то на разность. Эта домножаемая сумма или разность будет называться сопряженной к выражению, стоящему в знаменателе.Эффект этой схеме хорошо виден на примере: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2)-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = sqrt(2)-1.
4
Если в знаменателе присутствует сумма (разность), в которой присутствует корень большей степени, то ситуация становится нетривиальной и избавление от иррациональности в знаменателе не всегда возможно
Источники:
- избавиться от корня в знаменателе