Вам понадобится
  • Учебник по геометрии
Инструкция
1
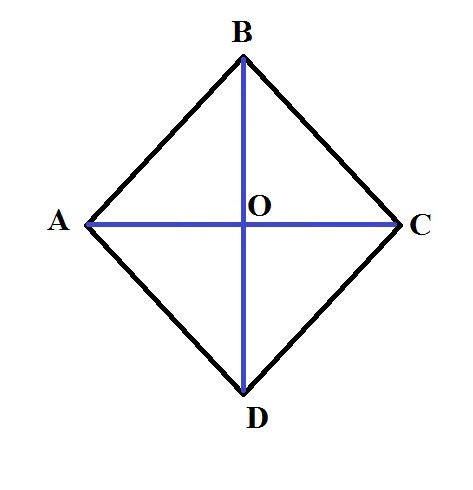
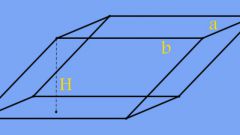
Для того, чтобы найти площадь ромба, нужно перемножить длины его диагоналей и разделить это произведение на два.
S = (AC*BD)/2.Пример: Пусть дан ромб АВСD. Длина его большей диагонали AC равна 3 см. Длина стороны АВ составляет 2 см. Найдите площадь этого ромба. Для того, чтобы решить данную задачу, необходимо найти длину второй диагонали. Для этого воспользуйтесь таким свойством, что сумма квадратов диагоналей ромба, равна сумме квадратов его сторон. То есть 4*AB^2 = AC^2+BD^2. Отсюда:
BD = 4*AB^2-AC^2;
BD = (4* 2^2-3^2)^0,5 = (7)^0,5 см;
Тогда S = (7)^0,5*3/2 = 3,97 см^2
2
Так как ромб является частным случаем параллелограмма, то его площадь можно найти, как произведение его стороны на высоту, опущенную из вершины любого угла: S = h*АВПример: Путь площадь ромба составляет 16 см^2, а длина его стороны 8 см. Найдите длину высоты, опущенную на одну из его сторон. По вышеприведенной формуле: S = h*AB, тогда, выразив высоту, получите:
h = S/AB;
h= 16/8= 2 см.
3
Другой способ нахождения площади ромба хорош, если известен какой-либо из углов углов, между двумя смежными сторонами. В этом случае целесообразно воспользоваться формулой: S = а*АВ^2, где а - это угол между сторонами.Пример: Пусть угол между двумя смежными сторонами составляет 60 градусов (угол DAB), а противолежащая диагональ DB равна 8 см. Найдите площадь ромба АВСD.Решение:
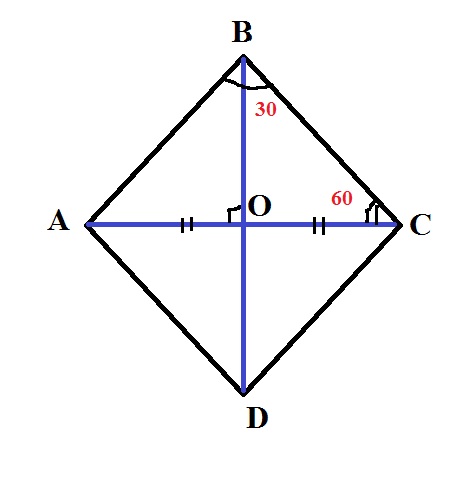
1. Диагональ AC является биссектрисой угла DAB и делит отрезок DB пополам, причем, пересекает его под прямым углом. Обозначьте точкой О место пересечения диагоналей.2. Рассмотрите треугольник AOB. Из пункта 1 следует, что он является прямоугольным, угол ВАО равен 30 градусам, длина катета ОВ составляет 4 см. 3. Известно, что катет, лежащий против угла в 30 градусов, равен половине гипотенузы (это утверждение получено из геометрического определения синуса). Следовательно длина АВ равна 8 см.4. Рассчитайте площадь ромба АВСD по формуле: S = sin(DAB)*АВ^2;
S = ((3)^0,5/2)*8^2 = 55,43 см^2.
Иллюстрация к примеру 2.