Инструкция
1
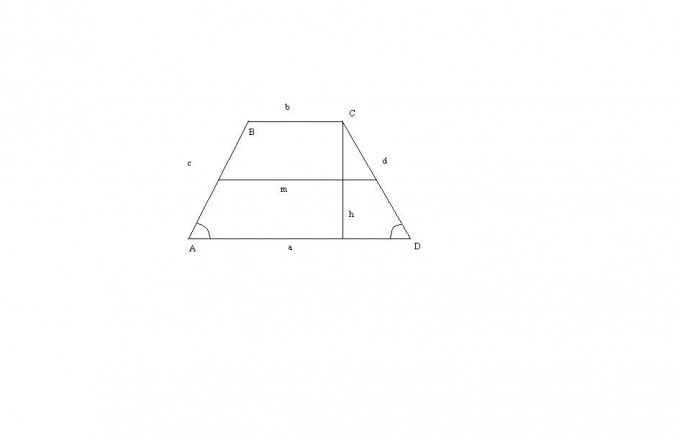
Четырехугольник, у которого пара противолежащих сторон параллельна, называют трапецией. В трапеции определяют основания, стороны, диагонали, высоту, среднюю линию. Зная различные элементы трапеции, можно найти ее площадь.
2
Иногда специальными случаями равнобедренных трапеций считаются прямоугольники и квадраты, но во многих источниках они к трапециям не относятся. Еще одним специальным случаем равнобедренной трапеции считается такая геометрическая фигура с 3 равными сторона. Ее называют трехсторонней трапецией, или триравнобедренной трапецией, или, реже, symtra. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон.
3
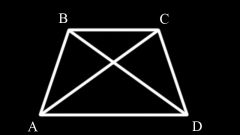
Трапеция состоит из оснований (параллельные противоположные стороны), боковых сторон (две другие стороны), средней линии (отрезок, соединяющий середины боковых сторон). Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
4
Чтобы трапеция считалась равнобедренной, должно выполняться как минимум одно из следующих условий. Первое: углы при основе трапеции должны быть равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC. Второе: диагонали трапеции должны быть равны: AC = BD. Третье: если углы между диагоналями и основаниями одинаковы, трапеция считается равнобедренной: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC. Четвертое: сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°. Пятое: если вокруг трапеции можно описать окружность, она считается равнобедренной.
5
Равнобедренная трапеция, как и любая другая геометрическая фигура, обладает рядом неизменных свойств. Первое из них: сумма углов, прилегающих к боковой стороне равнобедренной трапеции равна 180°: ∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°. Второе: если в равнобедренную трапецию можно вписать окружность, то ее боковая сторона равна средней линии трапеции: AB = CD = m. Третье: вокруг равнобедренной трапеции всегда можно описать окружность. Четвертое: если диагонали взаимно перпендикулярны, то высота трапеции равна полусумме оснований (средней линии): h=m. Пятое: если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты: SABCD = h2 . Шестое: если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции: h2 = BC • AD. Седьмое: сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции: AC2 + BD2 = AB2 + CD2 + 2BC • AD. Восьмое: прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции: HF ┴ BC ┴ AD. Девятое: высота ((CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) - равен полуразности оснований: AP=BC+AD/2, PD=AD-BC/2.
6
Самая распространенная формула для вычисления площади трапеции - S = (a+b)h/2. Для случая равнобедренной трапеции она явным образом не поменяется. Можно лишь отметить, что у равнобедренной трапеции углы при любом из оснований будут равны (DAB = CDA = x). Так как ее боковые стороны тоже равны (AB = CD = с), то и высоту h можно посчитать по формуле h = с*sin(x).

Тогда S = (a+b)*с*sin(x)/2.

Аналогично, площадь трапеции можно записать через среднюю сторону трапеции: S = mh.
7
Рассмотрим частный случай равнобедренной трапеции, когда ее диагонали перпендикулярны. В этом случае, по свойству трапеции, ее высота равна полусумме оснований.

Тогда площадь трапеции можно вычислить по формуле: S = (a+b)^2/4.
8
Рассмотрим также еще одну формулу для определения площади трапеции: S = ((a+b)/2)*sqrt(c^2 - ((b-a)^2+c^2-d^2)/2(b-a))^2), где c и d - боковые стороны трапеции. Тогда в случае равнобедренной трапеции, когда c = d, формула принимает вид: S = ((a+b)/2)*sqrt(c^2-((b-a)^2/2(b-a))^2).
9
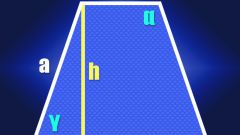
Найдите площадь трапеции по формуле S=0,5×(a+b)×h, если известны a и b — длины оснований трапеции, то есть параллельные стороны четырехугольника, и h — высота трапеции (наименьшее расстояние между основаниями). Например, пусть дана трапеция с основаниями a=3 см, b=4 см и высотой h=7 см. Тогда ее площадь будет равна S=0,5×(3+4)×7=24,5 см².
10
Воспользуйтесь следующей формулой для вычисления площади трапеции: S=0,5×AC×BD×sin(β), где AC и BD — диагонали трапеции, а β — угол между этими диагоналями. Например, задана трапеция с диагоналями AC=4 см и BD=6 см и углом β=52°, тогда sin(52°)≈0,79. Подставьте значения в формулу S=0,5×4×6×0,79≈9,5 см².
11
Посчитайте площадь трапеции, когда известны ее m — средняя линия (отрезок, соединяющий середины сторон трапеции) и h — высота. В этом случае площадь будет равна S=m×h. К примеру, пусть у трапеции средняя линия m=10 см, а высота h=4 см. В этом случае получается, что площадь заданной трапеции равна S=10×4=40 см².
12
Вычислите площадь трапеции, в случае когда даны длины ее боковых сторон и оснований по формуле: S=0,5×(a+b)×√(c²−(((b−a)²+c²−d²)÷(2×(b−a)))²), где a и b — основания трапеции, а c и d — ее боковые стороны. Например, пусть дана трапеция с основаниями 40 см и 14 см и боковыми сторонами 17 см и 25 см. По вышеуказанной формуле S=0,5×(40+14)×√(17²−(((14−40)²+17²−25²)÷(2×(14−40)))²)≈423,7 см².
13
Рассчитайте площадь равнобедренной (равнобокой) трапеции, то есть трапеции у которой боковые стороны равны, если в нее вписана окружность по формуле: S=(4×r²)÷sin(α), где r — радиус вписанной окружности, α — угол при основании трапеции. В равнобедренной трапеции углы при основании равны. Например, пусть в трапецию вписана окружность радиусом r=3 см, а угол при основании α=30°, тогда sin(30°)=0,5. Подставьте значения в формулу: S=(4×3²)÷0,5=72 см².