Вам понадобится
- Циркуль, линейка, карандаш
Инструкция
1
Пусть мы имеем отрезок. Рассмотрим, как построить серединный перпендикуляр к этому отрезку.
2
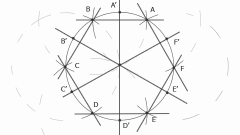
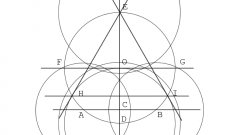
Через концы отрезка проведите две окружности с одинаковыми радиусами. Не обязательно строить всю окружность, достаточно получить только точки пересечения.
3
Через точки пересечения окружностей проведите прямую. Вы получили серединный перпендикуляр к заданному отрезку.
4
Пусть теперь нам задана точка и прямая. Необходимо провести перпендикуляр из этой точки к прямой.Поставьте иглу циркуля в точку. Проведите окружность произвольного радиуса (радиус должен быть больше расстояния от точки до прямой, чтобы окружность могла пересечь прямую в двух точках). Теперь вы имеете две точки на прямой. Эти точки создают отрезок. Постройте серединный перпендикуляр к отрезку, концами которого являются полученные точки, по алгоритму, рассмотренному выше. Перпендикуляр должен пройти через начальную точку.