Как решать матрицу методом гаусса

Решение матрицы в классическом варианте находится с помощью метода Гаусса. Данный метод основан на последовательном исключении неизвестных переменных. Решение выполняется для расширенной матрицы, то есть с включенным столбцом свободных членов. При этом коэффициенты, составляющие матрицу, в результате проведенных преобразований образуют ступенчатую или треугольную матрицу. Относительно главной диагонали все коэффициенты матрицы, кроме свободных членов, должны быть приведены к нулю.

Инструкция

1. Определите совместность системы уравнений. Для этого посчитайте ранг основной матрицы А, то есть без столбца свободных членов. Затем добавьте столбец свободных членов и вычислите ранг получившейся расширенной матрицы В. Ранг должен быть отличным от нуля, тогда система имеет решение. При равных значениях рангов существует единственное решение данной матрицы.
   
2. Приведите расширенную матрицу к виду, когда по главной диагонали располагаются единицы, а ниже нее все элементы матрицы равны нулю. Для этого первую строку матрицы разделите на ее первый элемент так, чтобы первый элемент главной диагонали стал равен единице.
   
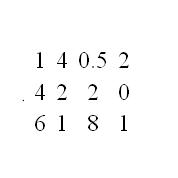
3. Отнимите первую строку от всех нижних строк так, чтобы в перовом столбце все нижние элементы обратились в ноль. Для этого помножьте сначала первую строку на первый элемент второй строки и отнимите строки. Затем аналогично помножьте первую строку на первый элемент третьей строки и отнимите строки. И так продолжайте со всеми строками матрицы.
   
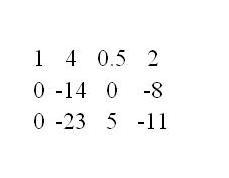
4. Разделите вторую строку на коэффициент во втором столбце так, чтобы следующий элемент главной диагонали на второй строке и во втором столбце стал равен единице.
   
5. Отнимите вторую строку от всех нижних строк таким же образом, как описано выше. Все нижестоящие относительно второй строки элементы должны обратиться в ноль.
   
6. Аналогично проведите образование следующей единички на главной диагонали в третьей и последующих строках и обнуление нижестоящих коэффициентов матрицы.
   
7. Затем приведите полученную треугольную матрицу к виду, когда элементы над главной диагональю также представляют собой нули. Для этого отнимите последнюю строку матрицы из всех вышестоящих строк. Домножайте на соответствующий коэффициент и вычитайте стоки так, чтобы обратились в ноль элементы столбца, где в текущей строке имеется единичка.
   
8. Проведите подобное вычитание всех строк в порядке снизу вверх, пока не обнулятся все элементы выше главной диагонали.
9. Оставшиеся элементы в столбце свободных членов и являются решением заданной матрицы. Запишите полученные значения.