Инструкция
1
Прочитайте очень внимательно условие задачи, если что-то не запомнили или не поняли, перечитайте еще раз.
2
Начертите чертеж к задаче на черновике. Проставьте на него все известные размеры, это необходимо сделать аккуратно, чтобы вы сами не запутались в этих данных.
3
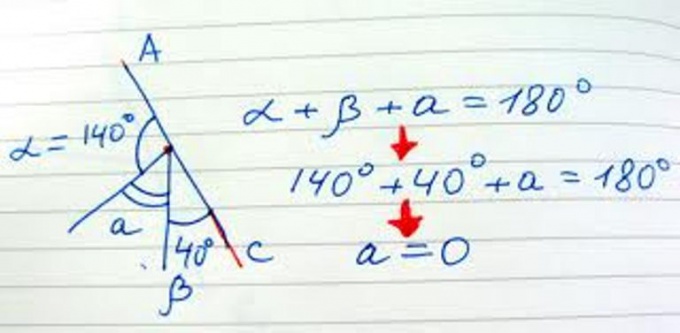
Постарайтесь определить, к какому виду геометрических задач она относится, так, например: вычислительные, когда нужно узнать какую-нибудь величину, задачи на доказательство, требующие логической цепочки рассуждений, задачи на построение при помощи циркуля и линейки. Еще бывают задачи смешанного типа. Когда вы выяснили тип задачи, постарайтесь рассуждать логически.
4
Примените необходимую теорему для решения данной задачи, если же есть сомнения или вообще отсутствуют варианты, то постарайтесь вспомнить теорию, которую вы проходили по соответствующей теме.
5
Оформите решение задачи также на черновике. Попытайтесь применить известные способы проверки верности вашего решения.
6
Оформите решение задачи аккуратно в тетради, без помарок и зачеркиваний, а главное - напишите ответ.Возможно, на решение первых геометрических задач уйдет много сил и времени. Однако, как только вы освоите этот процесс - начнете щелкать задачи по геометрии, как орешки, получая от этого удовольствие!