Инструкция
1
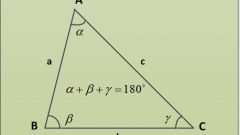
Многоугольник называется правильным, если его стороны равны между собой, а так же все углы равны между собой.
Если заранее известно, что многоугольник является правильным, то углы можно высчитать по формуле
?? = 180? * (n - 2)/n, где n – количество сторон многоугольника.
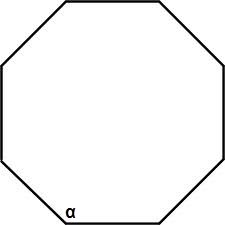
Например, в случае правильного восьмиугольника
?? = 180? * (8 - 2)/8 = 135?
Если заранее известно, что многоугольник является правильным, то углы можно высчитать по формуле
?? = 180? * (n - 2)/n, где n – количество сторон многоугольника.
Например, в случае правильного восьмиугольника
?? = 180? * (8 - 2)/8 = 135?
2
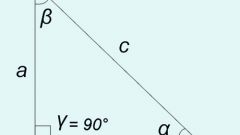
Для неправильного треугольника с известными сторонами, углы можно рассчитать по теореме косинусов, например, для угла ?? в приведённом рисунке формула примет вид
cos?? = (b? + c? - a?) / 2 • b • c
cos?? = (b? + c? - a?) / 2 • b • c

3
Для нахождения углов неправильных многоугольников с количеством сторон больше 3 наличие длин сторон не является достаточным условием.