Инструкция
1
Если в электрическое поле, создаваемое зарядом Q, поместить еще один заряд Q0, то оно будет воздействовать на него с определенной силой. Это характеристика называется напряженностью электрического поля E. Она представляет собой отношение силы F, с которое поле действует на положительный электрический заряд Q0 в определенной точке пространства, к значению этого заряда: E = F/Q0.
2
В зависимости от конкретной точки пространства, значение напряженности поля E может меняться, что выражается формулой Е = Е (x, y, z, t). Поэтому напряженность электрического поля относится к векторным физическим величинам.
3
Поскольку напряженность поля зависит от силой, действующей на точечный заряд, то вектор напряженности электрического поля E одинаков с вектором силы F. Согласно закону Кулона, сила, с которой взаимодействуют две заряженные частицы в вакууме, направлена по прямой линии, которая соединяет эти заряды.
4
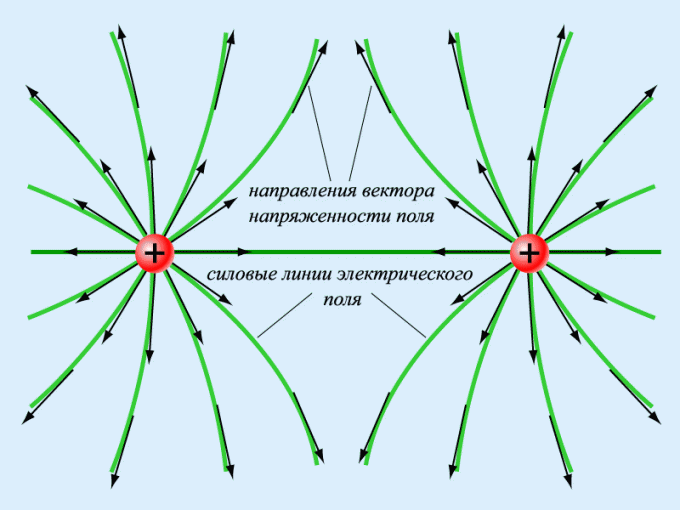
Майкл Фарадей предложил наглядно изображать напряженность поля электрического заряда с помощью линий напряженности. Эти линии совпадают с вектором напряженности во всех точках по касательной. На чертежах их принято обозначать стрелками.
5
В том случае, если электрическое поле однородно и вектор его напряженности постоянен по своему модулю и направлению, то линии напряженности параллельны с ним. Если электрическое поле создается положительно заряженным телом, линии напряженности направлены от него, а в случае с отрицательно заряженной частицей - по направлению к нему.
Обратите внимание
Вектор напряженности имеет лишь одно направление в каждой точке пространства, поэтому линии напряженности никогда не пересекаются.
Источники:
- Напряженность электрического поля