Инструкция
1
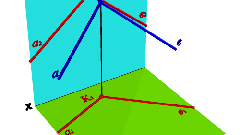
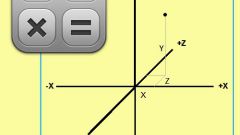
Для того, чтобы найти расстояние от точки до прямой, вам необходим перпендикуляр от этой точки до заданной прямой.
2
Посмотрите на чертеж, который вы нарисовали по условию задачи.
3
Если требуемый перпендикуляр от точки до прямой уже присутствует на чертеже (например, в условии сказано, что это перпендикуляр, высота, задан угол в 90 градусов), найдите его длину. Вам могут быть заданы длины других сторон, величины углов, свойства фигуры. Используйте теоремы геометрии.
4
Если вы видите, что требуемый перпендикуляр присутствует, но про него не известно, что это перпендикуляр, докажите, что он является именно перпендикуляром. Затем найдите его длину.
5
Если требуемого перпендикуляра еще нет, постройте его. Будьте внимательны и аккуратны при построении, помните о свойствах перпендикуляра. Построив перпендикуляр, подумайте, как можно найти его длину. Найдите длину перпендикуляра.
Видео по теме
Обратите внимание
Не путайте высоту с медианой и биссектрисой. В общем случае эти прямые не совпадают.
Полезный совет
В некоторых случаях построение перпендикуляра не требуется. Иногда найти высоту фигуры можно, исходя из свойств фигуры и применив формулу нахождения площади. Это в том случае, если расстоянием от точки до прямой является именно высота фигуры.
Источники:
- как найти расстояние от точки до сторон