Инструкция
1
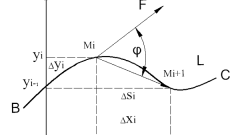
Наиболее часто встречаются задачи на определение радиуса кривизны траектории полета брошенного тела в заданный промежуток времени. Траектория движения в данном случае описывается уравнениями на координатных осях: х = f(t), y = f(t), где t – время, в момент которого требуется найти радиус. Его вычисление будет основываться на применении формулы аn = V²/R. Здесь радиус R выявляется из отношения нормального ускорения аn и мгновенной скорости V движения тела. Узнав данные величины, можно легко найти искомую компоненту R.
2
Вычислите проекции скорости тела на осях (ОХ, ОY). Математический смысл скорости – это первая производная от уравнения движения. Поэтому они легко находятся взятием производной от заданных уравнений: Vx = x', Vy = y'. При рассмотрении геометрического отображения данных проекций в координатной системе видно, что они являются катетами прямоугольного треугольника. Причем гипотенуза в нем – искомая мгновенная скорость. Исходя из этого, вычислите величину мгновенной скорости V по теореме Пифагора: V = √( Vx² + Vy²). Подставляя в выражение известное значение времени, найдите числовой показатель V.
3
Модуль нормального ускорения также легко определить, рассмотрев другой прямоугольный треугольник, образуемый модулем полного ускорения а и касательного ускорения тела ак. Причем здесь нормальное ускорение является катетом и вычисляется так: аn = √( а² - ак²). Для нахождения касательного ускорения продифференцируйте по времени уравнение мгновенной скорости движения: ак = |dV/dt|. Полное же ускорение вычислите по его проекциям на оси, аналогично нахождению мгновенной скорости. Только для этого возьмите от заданных уравнений движения производные второго порядка: ах = х'', аy = y''. Модуль ускорения а = √( ах2 + аy2). Подставляя все найденные величины, определите числовое значение нормального ускорения аn = √( а² - ак²).
4
Выразите из формулы аn = V²/R искомую переменную радиуса кривизны траектории: R = V²/ аn. Подставьте числовые значения скорости и ускорения, вычислите радиус.