Вам понадобится
- - формула расчета центра масс.
Инструкция
1
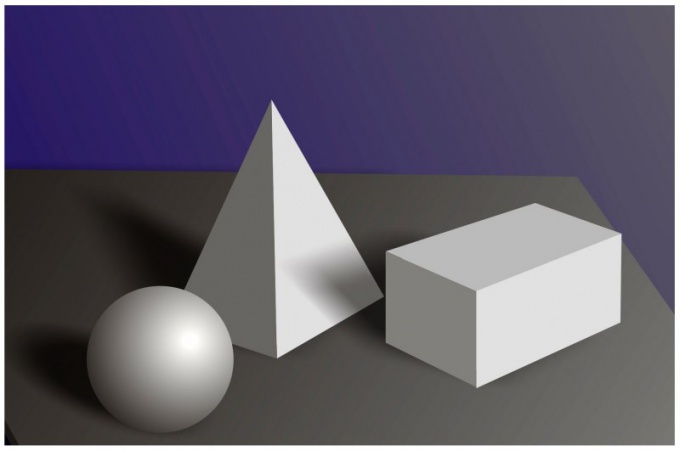
Следует учитывать, что положение центра масс напрямую зависит от того, каким образом распределена по объему тела его масса. Центр масс может даже не находиться в самом теле, примером такого объекта может служить однородное кольцо, у которого центр масс находится в его геометрическом центре. То есть – в пустоте. При расчетах центр масс можно расценивать математической точкой, в которой сосредоточена вся масса тела.
2
Понятия центра масс и центра тяжести тела очень близки, поэтому при расчетах, в большинстве случаев, их можно считать синонимами. Отличие лишь в том, что для понятия центра тяжести необходимо наличие тяготения, а центр масс присутствует и при отсутствии силы тяжести. Тело, падающее свободно и без вращения, движется под действием силы тяготения, приложенной ко всем его точкам, при этом его центр масс совпадает с центром тяжести. Для определения центра масс в классической механике используется приведенная ниже формула.
3
Здесь R.ц.м. – радиус-вектор центра масс, mi – масса i-той точки, ri – радиус-вектор i-той точки системы. На практике во многих случаях легко найти центр масс, если предмет имеет некую строгую геометрическую форму. Например, у однородного стержня он находится точно посередине. У параллелограмма - на пересечении диагоналей, у треугольника это точка пересечения медиан, а у правильного многоугольника центр масс находится в центре поворотной симметрии.
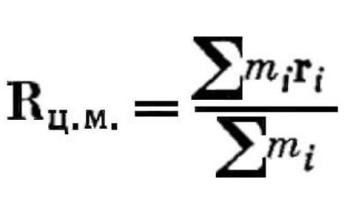
4
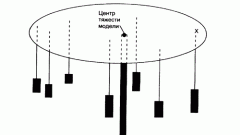
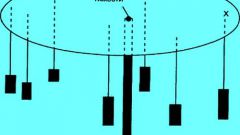
Для более сложных тел задача расчета усложняется, в этом случае необходимо разбить объект на однородные объемы. Для каждого из них отдельно высчитываются центры масс, после чего найденные значения подставляются в соответствующие формулы и находится итоговое значение.
5
На практике необходимость определения центра масс (центра тяжести) обычно связана с конструкторскими работами. Например, при проектировании судна важно обеспечить его остойчивость. Если центр тяжести будет находиться очень высоко, то судно может опрокинуться. Как рассчитать нужный параметр для такого сложного объекта, как судно? Для этого находятся центры тяжести его отдельных элементов и агрегатов, после чего найденные значения складываются с учетом их месторасположения. При конструировании центр тяжести обычно стараются расположить как можно ниже, поэтому наиболее тяжелые агрегаты располагают в самом низу.
Источники:
- Центр масс
- Решение задач по физике