Как найти высоту пирамиды

Любое геометрическое тело может быть интересно не только школьнику. В окружающем мире довольно часто встречаются предметы в форме пирамиды. И это не только знаменитые египетские гробницы. Часто говорят о целебных свойствах пирамиды, и кому-то наверняка захочется испытать их на себе. Но для этого надо знать ее размеры, в том числе высоту.

Вам понадобится

• Математические формулы и понятия:
• Определение высоты пирамиды
• Признаки подобия треугольников
• Свойства высоты треугольника
• Теорема синусов и косинусов
• Таблицы синусов и косинусов
• Инструменты:
• линейка
• карандаш
• транспортир

Инструкция

1. Вспомните, что такое высота пирамиды. Это есть перпендикуляр, опущенный из вершины пирамиды к ее основанию.
   
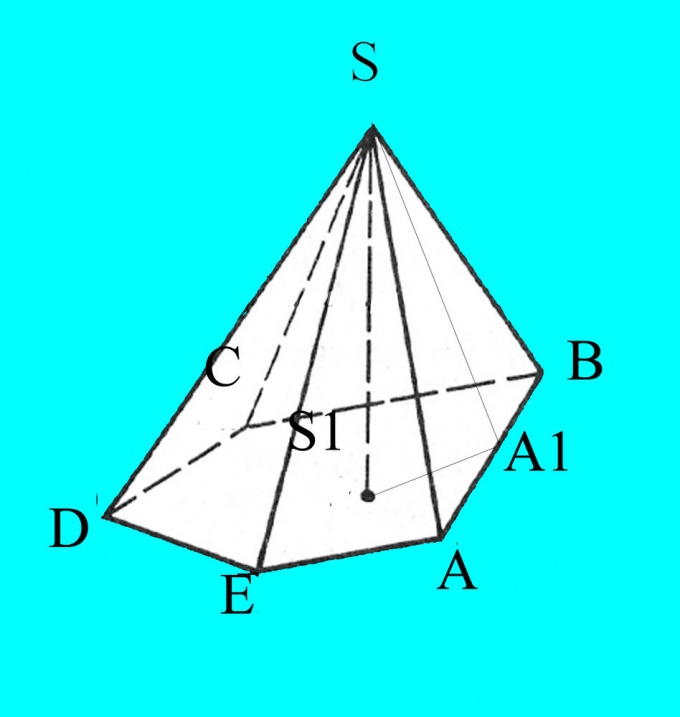
2. Постройте пирамиду по заданным параметрам. Обозначьте ее основание латинскими буквами А, B, C,D... в зависимости от количества углов. Вершину пирамиды обозначьте S.
3. Вам известны стороны, углы основания и наклона ребер к основанию. Чертеж получится в проекции на плоскости, поэтому для верности обозначьте на нем известные вам данные. Из точки S опустите высоту пирамиды и обозначьте ее h. Точку пересечения высоты с основанием пирамиды обознчьте S1.
4. Из вершины пирамиды проведите высоту любой боковой грани. Обозначьте точку ее пересечения с основанием, например, А1. Вспомните свойства высоты остроугольного треугольника. Она делит треугольник на два подобных прямоугольных треугольника. Вычислите косинусы нужных вам углов по формуле
   
   Cos(A) = (b2+c2-a2)/(2*b*c), где а,b и с - стороны треугольника, в данном случае АSB (a=BA,b=AS,c=AB).
   
   Вычислите высоту боковой грани SA1 по косинусу угла АSA1, равного углу SBA из свойств высоты треугольника, и известному боковому ребру AS.
5. Соедините точки А1 и S1. У вас получился прямоугольный треугольник, в котором вам известна гипотенуза SA1 и угол наклона боковой грани пирамиды к ее основанию SA1S1. По теореме синусов вычислите катет SS1, который одновременно является и высотой пирамиды.