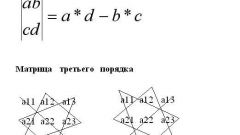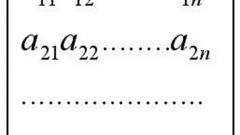Инструкция
1
Суммой матриц A = (aij) и B = (bij) называется матрица C = (cij) такой же размерности , где ее элементы cij определяются равенством cij = aij + bij (i = 1, 2, …, m; j = 1, 2 …, n).
Сложение матриц обладает следующими свойствами:
1. A + B = B + A
2. (A + B) + C = A + (B + C)
Сложение матриц обладает следующими свойствами:
1. A + B = B + A
2. (A + B) + C = A + (B + C)
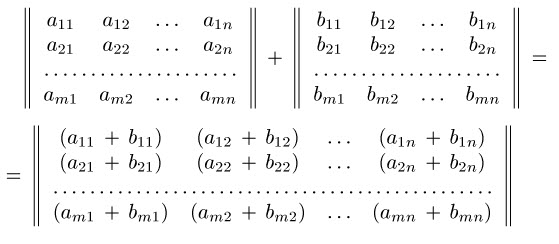
2
Произведением матрицы A = (aij) на действительное число ? называется матрица C = (cij), где ее элементы cij определяются равенством cij = ? * aij (i = 1, 2, …, m; j = 1, 2 …, n).
Умножение матрицы на число обладает следующими свойствами:
1. (??)A = ?(?A), ? и ? – действительные числа,
2. ?(А + В) = ?А + ?В, ? – действительное число,
3. (? + ?)В = ?В + ?В, ? и ? – действительные числа.
Введя операцию умножения матрицы на скаляр, можно ввести операцию вычитания матриц. Разностью матриц A и B будет матрица C, которую можно вычислить по правилу:
C = A + (-1)*B
Умножение матрицы на число обладает следующими свойствами:
1. (??)A = ?(?A), ? и ? – действительные числа,
2. ?(А + В) = ?А + ?В, ? – действительное число,
3. (? + ?)В = ?В + ?В, ? и ? – действительные числа.
Введя операцию умножения матрицы на скаляр, можно ввести операцию вычитания матриц. Разностью матриц A и B будет матрица C, которую можно вычислить по правилу:
C = A + (-1)*B
3
Произведение матриц. Матрицу A можно умножить на матрицу B, если число столбцов матрицы A равно числу строк матрицы B.
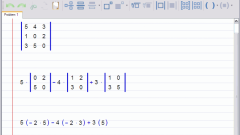
Произведением матрицы A = (aij) размерности m*n на матрицу B = (bij) размерности n*p называется матрица C = (cij) размерности m*p, где её элементы cij определяются по формуле cij = ai1*b1j + ai2*b2j + … + ain*bnj (i = 1, 2, …, m; j = 1, 2 …, p).
На рисунке приведён пример произведения матриц размерности 2*2.
Произведение матриц обладает следующими свойствами:
1. (A * B) * C = A * (B * C)
2. (A + B) * C = A*C + B*C или A * (B + C) = A*B + A*C
Произведением матрицы A = (aij) размерности m*n на матрицу B = (bij) размерности n*p называется матрица C = (cij) размерности m*p, где её элементы cij определяются по формуле cij = ai1*b1j + ai2*b2j + … + ain*bnj (i = 1, 2, …, m; j = 1, 2 …, p).
На рисунке приведён пример произведения матриц размерности 2*2.
Произведение матриц обладает следующими свойствами:
1. (A * B) * C = A * (B * C)
2. (A + B) * C = A*C + B*C или A * (B + C) = A*B + A*C
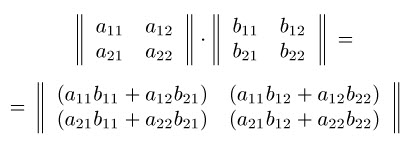
Видео по теме
Источники:
- матрица считать