Как найти площадь пирамиды

Пирамида - сложное геометрическое тело. Оно образовано плоским многоугольником (основание пирамиды), точкой, не лежащей в плоскости этого многоугольника (вершина пирамиды) и всех отрезков, которые соединяют точки основания пирамиды с вершиной. Как же найти площадь пирамиды?

Вам понадобится

• линейка, карандаш и бумага

Инструкция

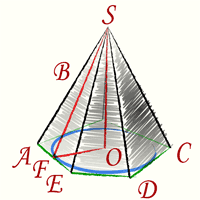
1. Площадь боковой поверхности любой пирамиды равна сумме площадей её боковых граней.
   
   Т.к. все боковые грани пирамиды треугольники, то надо найти сумму площадей всех этих треугольников. Площадь треугольника вычисляется путем умножения длины основания треугольника на длину его высоты.
   
2. Основанием пирамиды является многоугольник. Если данный многоугольник поделить на треугольники, то площадь многоугольника просто вычислить как сумму площадей получившмхся при делении треугольников по уже известной нам формуле.
3. Найдя сумму площадей боковой поверхности пирамиды и основания пирамиды, можно найти общую площадь поверхности пирамиды.
4. Для вычислений площади правильной пирамиды пользуются специальной формулой.
   
   Пример:
   
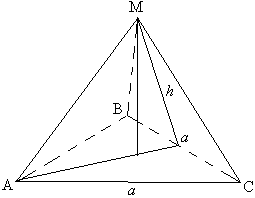
   Перед нами правильная пирамида. В основании находится правильный n-угольник со стороной а. Высота боковой грани - h (кстати, имеет название апофема пирамиды). Площадь каждой боковой грани равна 1/2ah. Вся боковая поверхность пирамиды имеет площадь n/2ha, вычисляем путем сложения площадей боковых граней. na - это периметр основания пирамиды. Площадь этой пирамиды найдем так: произведение апофемы пирамиды и половины периметра её основания равно площади боковой поверхности правильной пирамиды.
5. Что касается площади полной поверхности, то просто к боковой прибавляем площадь основания, по принципу, рассмотренному выше.