Инструкция
1
Для перевода восьмиричного числа в двоичную систему необходимо каждую его цифру представить в виде триад двоичных цифр. Например, восьмиричное число 765 раскладывается на триады следующим образом: 7 = 111, 6 = 110, 5 = 101. В итоге получается двоичное число 111110101.
2
Для в двоичную систему счисления необходимо каждую его цифру представить в виде тетрады двоичных цифр. Например, шестнадцатиричное число 967 раскладывается на тетрады следующим образом: 9 = 1001, 6 = 0110, 7 = 0111. В итоге получается двоичное число 100101100111.
3
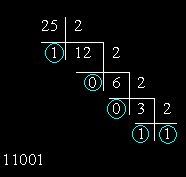
Чтобы десятичное число перевести в двоичную систему счисления, необходимо последовательно делить его на два, каждый раз записывая результат в виде целого числа и остатка. Деление нужно продолжать до тех пор, пока не останется число равное единице. Итоговое число получается путём последовательной записи результата последнего деления и остатков всех делений в обратном порядке. В качестве примера на рисунке показана процедура перевода десятичного числа 25 в двоичную систему счисления. Последовательное деление на два даёт следующую последовательность остатков: 10011. Развернув её наоборот, получим искомое число.
Обратите внимание
Поэтому, получив в результате серии умножений на 2 справа от вертикали одни нули, мы заканчиваем процесс перевода десятичного дробного числа меньше единицы в двоичную систему счисления и записываем ответ: Понятно, что гораздо чаще мы встретим такую исходную десятичную дробь, когда умножение на 2 чисел, стоящих справа от вертикали, не приведет к появлению там одних лишь нулей.
Полезный совет
Мы уже знаем, как переводить числа в различные системы счисления. Посмотрим, как это происходит с двоичной системой счисления. Переведём число из двоичной системы счисления в десятичную. Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой.
Источники:
- двоичная система счисления перевод