Инструкция
1
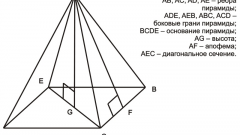
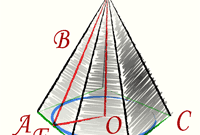
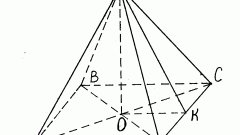
Рассматривайте ребра пирамиды как векторы, на которых построена эта фигура. По координатам точек в вершинах A(X₁;Y₁;Z₁), B(X₂;Y₂;Z₂), C(X₃;Y₃;Z₃), D(X₄;Y₄;Z₄), определите проекции векторов, исходящих из вершины пирамиды, на оси ортогональной системы координат - вычтите из каждой координаты конца вектора соответствующую координату начала: AB{X₂-X₁;Y₂-Y₁;Z₂-Z₁}, AC{X₃-X₁;Y₃-Y₁;Z₃-Z₁}, AD{X₄-X₁;Y₄-Y₁;Z₄-Z₁}.
2
Воспользуйтесь тем, что объем параллелепипеда, построенного на этих же векторах, должен быть в шесть раз больше объема пирамиды. Объем такого параллелепипеда определить нетрудно - он равен смешанному произведению векторов: |AB*AC*AD|. Значит, объем пирамиды (V) составит одну шестую часть от этой величины: V = ⅙*|AB*AC*AD|.
3
Для расчета смешанного произведения из полученных на первом шаге координат составьте матрицу, поместив в каждую ее строку три координаты соответствующего вектора:
(X₂-X₁) (Y₂-Y₁) (Z₂-Z₁)
(X₃-X₁) (Y₃-Y₁) (Z₃-Z₁)
(X₄-X₁) (Y₄-Y₁) (Z₄-Z₁)
Затем рассчитайте ее определитель - построчно перемножьте все элементы множества и сложите результаты:
(X₂-X₁)*(Y₃-Y₁)*(Z₄-Z₁) + (Y₂-Y₁)*(Z₃-Z₁)*(X₄-X₁) + (Z₂-Z₁)*(X₃-X₁)*(Y₄-Y₁) + (Z₂-Z₁)*(Y₃-Y₁)*(X₄-X₁) + (Y₂-Y₁)*(X₃-X₁)*(Z₄-Z₁) + (X₂-X₁)*(Z₃-Z₁)*(Y₄-Y₁).
(X₂-X₁) (Y₂-Y₁) (Z₂-Z₁)
(X₃-X₁) (Y₃-Y₁) (Z₃-Z₁)
(X₄-X₁) (Y₄-Y₁) (Z₄-Z₁)
Затем рассчитайте ее определитель - построчно перемножьте все элементы множества и сложите результаты:
(X₂-X₁)*(Y₃-Y₁)*(Z₄-Z₁) + (Y₂-Y₁)*(Z₃-Z₁)*(X₄-X₁) + (Z₂-Z₁)*(X₃-X₁)*(Y₄-Y₁) + (Z₂-Z₁)*(Y₃-Y₁)*(X₄-X₁) + (Y₂-Y₁)*(X₃-X₁)*(Z₄-Z₁) + (X₂-X₁)*(Z₃-Z₁)*(Y₄-Y₁).
4
Полученное на предыдущем шаге значение соответствует объему параллелепипеда - разделите его на шестерку, чтобы получить искомый объем пирамиды. В общем виде эту громоздкую формулу можно записать так: V = ⅙*|AB*AC*AD| = ⅙*((X₂-X₁)*(Y₃-Y₁)*(Z₄-Z₁) + (Y₂-Y₁)*(Z₃-Z₁)*(X₄-X₁) + (Z₂-Z₁)*(X₃-X₁)*(Y₄-Y₁) + (Z₂-Z₁)*(Y₃-Y₁)*(X₄-X₁) + (Y₂-Y₁)*(X₃-X₁)*(Z₄-Z₁) + (X₂-X₁)*(Z₃-Z₁)*(Y₄-Y₁)).
5
Если ход вычислений в решении задачи приводить не требуется, а нужно лишь получить численный результат, проще воспользоваться для расчетов онлайн-сервисами. В сети нетрудно найти скрипты, которые могут помочь с промежуточными расчетами - посчитать детерминант матрицы - или самостоятельно вычислить объем пирамиды по введенным в поля формы координатам точек. Пара ссылок на такие сервисы приведена ниже.
Источники:
- Расчет объема пирамиды по координатам
- объем пирамиды через координаты вершин