Как определить тип кривой второго порядка

Ответ весьма прост. Преобразуйте общее уравнение кривой второго порядка к каноническому виду. Искомых кривых всего три, и это эллипс, гипербола и парабола. Вид соответствующих уравнений можно увидеть в дополнительных источниках. Там же можно убедиться, что полную процедуру приведения к каноническому виду следует всячески избегать в силу ее громоздкости.

Инструкция

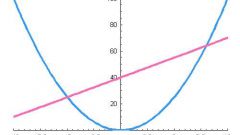
1. Вопрос о выяснении вида кривой второго порядка - скорее качественная, чем количественная задача. В самой общей случае решение может начинаться с заданного уравнения линии второго порядка (см. рис. 1). В этом уравнении все коэффициенты - некоторые постоянные числа. Если забыли уравнения эллипса, гиперболы и параболы в каноническом виде, посмотрите их в дополнительных источниках к этой статье или любом учебнике.
   
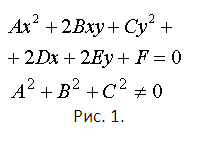
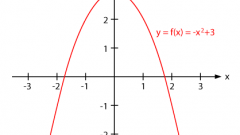
2. Сравните общее уравнение с каждым из тех канонических. Нетрудно придти к выводу, что если коэффициенты A≠0, С≠0, и их знак одинаков, то после любого преобразования, приводящего к каноническому виду, будет получен эллипс. Если знак различен – гипербола. Парабола же будет соответствовать ситуации, когда коэффициенты или А или С (но не оба сразу) равны нулю. Таким образом, ответ получен. Только вот числовых характеристик нет, кроме тех коэффициентов, что имеются в конкретном условии задачи.
3. Есть еще один способ получения ответа на поставленный вопрос. Это применение общего полярного уравнения кривых второго порядка. Это означает, что в полярных координатах все три, укладывающиеся в канон кривые (для декартовых координат) записываются практически одним и тем же уравнением. И хотя это в канон и не укладывается – здесь возможно список кривых второго порядка расширять неограниченно (апликата Бернулли, фигура Лиссажу и т. д.).
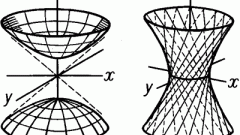
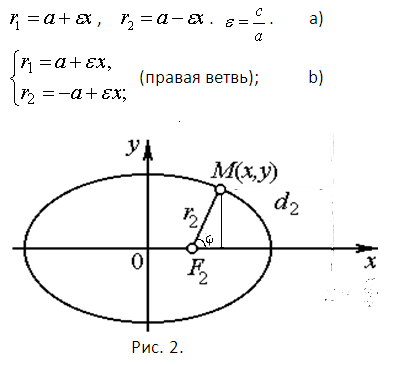
4. Ограничимся эллипсом (в основном) и гиперболой. Парабола возникнет автоматически, как случай промежуточный. Дело в том, что изначально эллипс определялся как геометрическое место точек, для которых сумма фокальных радиусов r1+r2=2a =const. Для гиперболы |r1-r2|=2a=const. Положите фокусы эллипса (гиперболы) F1(-c, 0), F2(c, 0). Тогда фокальные радиусы эллипса равны (см. рис. 2а). Для правой ветви гиперболы смотрите рисунок 2b.
   
5. Полярные координаты ρ=ρ(φ) следует вводить, используя фокус, как полярный центр. Тогда можно положить ρ=r2 и после незначительных преобразований получите для правых участков эллипса и параболы полярные уравнения (см. рис. 3). При этом а – большая полуось эллипса (мнимая для гиперболы), с – абсцисса фокуса, про параметр b – на рисунке.
   
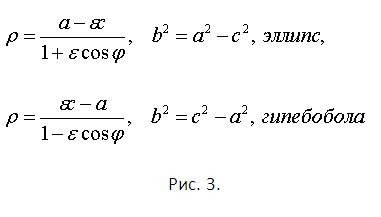
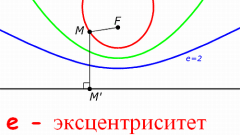
6. Приведенная на формулах рисунка 2 величина ε называется эксцентриситетом. Из формул рисунка 3 следует, что все прочие величины с ней как-либо связаны. И действительно, поскольку ε связана со всеми главными кривыми второго порядка, то на ее основе и можно принимать основные решения. А именно, если ε1 – гипербола. ε=1 – парабола. Это имеет и более глубокий смысл. В куда как крайне сложном курсе «Уравнения математической физики» классификация дифференциальных уравнений с частными производными производится на этой же основе.