Как определить натуральную величину треугольника

Вращающиеся геометрические фигуры занимают определенное положение по отношению к неподвижной системе. Зная данные вращающегося треугольника, несложно определить натуральную величину этой фигуры.

Вам понадобится

• - карандаш;
• - тетрадь.

Инструкция

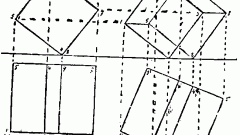
1. Найти натуральную величину треугольника можно методом замены плоскостей проекции. Для этого геометрическую фигуру представьте в виде плоскости уровня, когда одна из протекций отображена без искажений по отношению к плоскости.
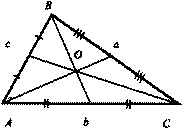
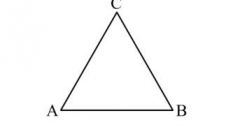
2. Первым делом по заданным координатам точек постройте проекцию треугольника ABC. Затем проведите фронтальную проекцию горизонтали этого треугольника, характеризующуюся точками B2 и M2. После этого по связующей линии найдите горизонтальную проекцию точки M1.
3. Чтобы треугольник стал проецирующим, введите дополнительную плоскость П4, которая будет перпендикулярна плоскости П1. При этом ось х1,4 расположена должна быть перпендикулярно проекции B1M1.
4. Из каждой точки горизонтальной плоскости проведите связующие линии, перпендикулярные оси х1,4. Для преобразования треугольника в плоскость уровня введите еще одну плоскость – П5. Ось х4,5 расположена будет параллельно A4B4C4.
5. Из каждой точки A4B4C4 проведите связующие линии, которые будут перпендикулярны оси х4,5. На этих линиях отложите расстояния, равные расстоянию от оси х1,4 до горизонтальной проекции каждой точки.
6. Треугольник ABC занял положение, которое параллельно плоскости П5. Проекция A5B5C5 – натуральная величина треугольника ABC.
7. Определить натуральную величину треугольника можно также и методом вращения. Для этого треугольник сначала представьте в виде проецирующей плоскости, после чего поверните его вокруг второй заданной оси, преобразовав его в плоскость уровня.