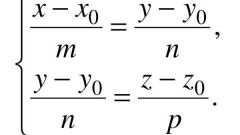Инструкция
1
Прямая – одно из фундаментальных геометрических понятий наряду с точкой и плоскостью. Это бесконечная фигура, которой можно соединить любые две точки в пространстве. Прямая всегда принадлежит какой-либо плоскости. Исходя из расположения двух прямых, следует применять разные методы поиска расстояния между ними.
2
Существует три варианта расположения двух прямых в пространстве друг относительно друга: они параллельны, пересекаются или скрещиваются. Второй вариант возможен, только если они лежат в одной плоскости, первый не исключает принадлежности двум параллельным плоскостям. Третья ситуация говорит о том, что прямые лежат в разных параллельных плоскостях.
3
Чтобы найти расстояние между двумя параллельными прямыми, нужно определить длину перпендикулярного отрезка, соединяющего их в любых двух точках. Поскольку прямые имеют две одинаковые координаты, что следует из определения их параллельности, то уравнения прямых в двухмерном координатном пространстве можно записать так:
L1: а•х + b•у + с = 0;
L2: а•х + b•у + d = 0.
Тогда можно найти длину отрезка по формуле:
s = |с - d|/√(a² + b²), причем нетрудно заметить, что при С = D, т.е. совпадении прямых, расстояние будет равно нулю.
L1: а•х + b•у + с = 0;
L2: а•х + b•у + d = 0.
Тогда можно найти длину отрезка по формуле:
s = |с - d|/√(a² + b²), причем нетрудно заметить, что при С = D, т.е. совпадении прямых, расстояние будет равно нулю.
4
Понятно, что расстояние между пересекающимися прямыми в двухмерной системе координат не имеет смысла. Зато когда они расположены в разных плоскостях, его можно найти как длину отрезка, лежащего в плоскости, перпендикулярной им обеим. Концами этого отрезка будут точки, являющиеся проекциями любых двух точек прямых на эту плоскость. Иными словами, его длина равна расстоянию между параллельными плоскостями, содержащими эти прямые. Таким образом, если плоскости заданы общими уравнениями:
α: А1•х + В1•у + С1•z + Е = 0,
β: А2•х + В2•у + С2•z + F = 0,
расстояние между прямыми можно вычислить по формуле:
s = |Е – F|/√(|А1•А2| + В1•В2 + С1•С2).
α: А1•х + В1•у + С1•z + Е = 0,
β: А2•х + В2•у + С2•z + F = 0,
расстояние между прямыми можно вычислить по формуле:
s = |Е – F|/√(|А1•А2| + В1•В2 + С1•С2).
Обратите внимание
Прямые вообще и скрещивающиеся в частности интересны не только математикам. Их свойства полезны во многих других областях: в строительстве и архитектуре, в медицине и в самой природе.