Вам понадобится
- - линейка;
- - карандаш;
- - циркуль.
Инструкция
1
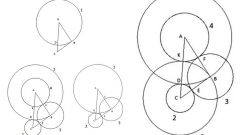
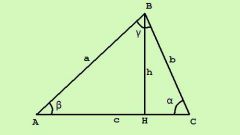
По теореме центром описанной окружности является центр пересечения серединных перпендикуляров. На рисунке видно, что каждая сторона треугольника, перпендикуляр, проведенный из ее середины и отрезки, соединяющие точку пересечения перпендикуляров с вершинами, образуют два равных прямоугольных треугольника. Отрезки MА, MВ, MС равны.
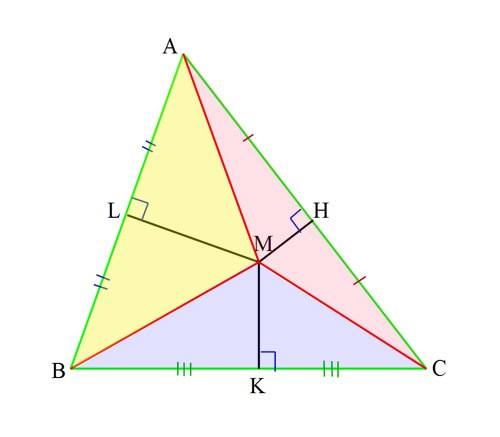
2
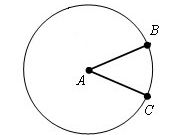
Вам дан треугольник. Найдите середину каждой стороны – возьмите линейку и измерьте его стороны. Полученные размеры разделите пополам. Отложите от вершин на каждой стороне половину ее размера. Отметьте результаты точками.
3
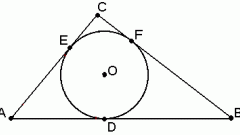
Из каждой точки отложите перпендикуляр к стороне. Точка пересечения этих перпендикуляров будет центром описанной окружности. Для нахождения центра окружности достаточно двух перпендикуляров. Третий строится для самопроверки.
4
5
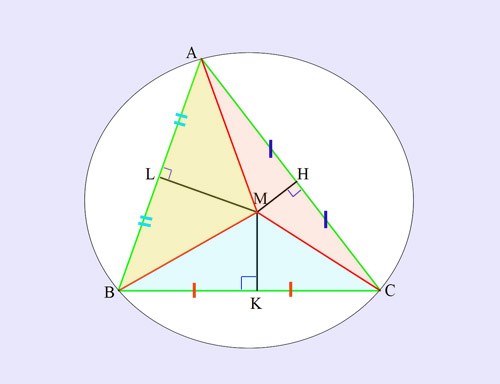
Измерьте расстояние от точки пересечения перпендикуляров до любой вершины треугольника. Установите это значение на циркуле. Поместив иглу в точку пересечения, начертите окружность. Если она касается всех трех вершин треугольника, вы все сделали правильно.
Обратите внимание
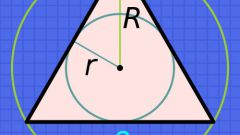
Существует теорема синусов, устанавливающая зависимость между сторонами треугольника, его углами и радиусами описанной окружности. Эта зависимость выражается формулой: a/sina = b/sinb = с/sinc = 2R, где a, b, c – стороны треугольника; sina, sinb, sinc – синусы углов, противолежащих этим сторонам; R – радиус окружности, которую можно описать вокруг треугольника.
Источники:
- как описать окружность четырехугольника