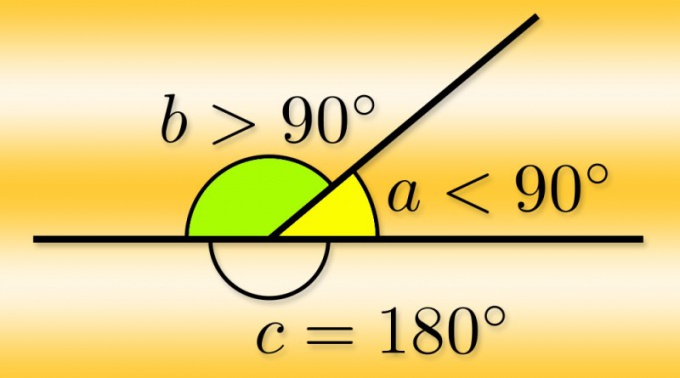Инструкция
1
Если вам известна величина основного угла (α) в градусах, рассчитать градусную меру любого из пары смежных (α₁ и α₂) будет очень просто. Каждый из них дополняет основной угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого числа известную величину основного угла α₁ = α₂ = 180°-α.
2
Величина исходного угла может быть приведена в радианах. Если и результат нужно получить в этих единицах, исходите из того, что развернутому углу соответствует количество радиан, равное числу Пи. Значит, формулу вычисления можно записать в таком виде: α₁ = α₂ = π-α.
3
Вместо градусной или радианной меры основного угла в условиях может быть дано соотношение величин основного и смежного углов. В этом случае составьте уравнение пропорции. Например, обозначьте через Y величину доли пропорции, относящуюся к основному углу, через X - относящуюся к смежному, а количество градусов, приходящееся на каждую единицу пропорции, обозначьте через k. Тогда общую формулу можно будет записать так: k*X+k*Y=180° или k*(X+Y)=180°. Выразите из нее общий множитель: k=180°/(X+Y). Затем рассчитайте величину смежного угла, умножив полученный коэффициент на долю этого угла в заданной пропорции: k*X = 180°/(X+Y)*X. Например, если это соотношение равно 5/13, величина смежного угла должна составлять 180°/(5+13)*13 = 10°*13 = 130°.
4
Если в исходных условиях ничего не сказано об основном угле, но дана величина вертикального угла, для вычисления смежных углов используйте формулы двух предыдущих шагов. Согласно определению вертикальный угол образуется двумя лучами, исходящими из той же точки, что и лучи основного угла, но направленными в строго противоположные стороны. Это значит, что градусная или радианная мера основного и вертикального угла равны, а значит, равны и величины смежных им углов.