Инструкция
1
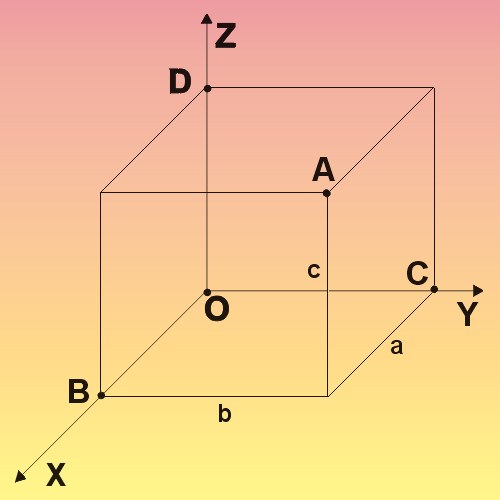
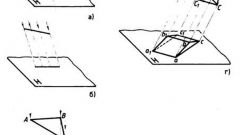
Рассмотрите прямую, проходящую через точку A₁(X₁;Y₁;Z₁), координаты которой известны из условий задачи, и ее проекцию на плоскость Aₒ(Xₒ;Yₒ;Zₒ), координаты которой нужно определить. Эта прямая должна быть перпендикулярна плоскости, поэтому в качестве направляющего вектора используйте нормальный к плоскости вектор. Плоскость задается уравнением a*X + b*Y + c*Z - d = 0, значит, нормальный вектор можно обозначить как ā = {a;b;c}. Исходя из этого вектора и координат точки, составьте канонические уравнения рассматриваемой прямой: (X-X₁)/a=(Y-Y₁)/b=(Z-Z₁)/c.
2
Найдите точку пересечения прямой с плоскостью, записав полученные в предыдущем шаге уравнения в параметрической форме: X = a*t+X₁, Y = b*t+Y₁ и Z = c*t+Z₁. Эти выражения подставьте в известное из условий уравнение плоскости, чтобы такое значение параметра tₒ, при котором прямая пересекает плоскость:a*(a*tₒ+X₁) + b*(b*tₒ+Y₁) + c*(c*tₒ+Z₁) - d = 0Преобразуйте его так, чтобы в левой части равенства осталась только переменная tₒ:a²*tₒ + a*X₁ + b²*tₒ + b*Y₁ + c²*tₒ + c*Z₁ - d = 0a²*tₒ + b²*tₒ + c²*tₒ = d - a*X₁ - b*Y₁ - c*Z₁tₒ*(a² + b² + c²) = d - a*X₁ - b*Y₁ - c*Z₁tₒ = (d - a*X₁ - b*Y₁ - c*Z₁)/(a² + b² + c²)
3
Подставьте полученное значение параметра для точки пересечения в уравнения проекций на каждую координатную ось из второго шага:Xₒ = a*tₒ+X₁ = a*((d - a*X₁ - b*Y₁ - c*Z₁)/(a² + b² + c²)) + X₁Yₒ = b*tₒ+Y₁ = b*((d - a*X₁ - b*Y₁ - c*Z₁)/(a² + b² + c²)) + Y₁Zₒ = c*tₒ+Z₁ = c*((d - a*X₁ - b*Y₁ - c*Z₁)/(a² + b² + c²)) + Z₁Рассчитанные по этим формулам величины и будут значениями абсциссы, ординаты и аппликаты точки проекции. Например, если исходная точка A₁ задана координатами (1;2;-1), а плоскость определена формулой 3*X-Y+2*Z-27 = 0, координаты проекции этой точки будут равны:Xₒ = 3*((27 - 3*1 - (-1*2) - 2*(-1))/(3² + (-1²) + 2²)) + 1 = 3*28/14 + 1 = 7Yₒ = -1*((27 - 3*1 - (-1*2) - 2*(-1))/(3² + (-1²) + 2²)) + 2 = -1*28/14 + 2 = 0Zₒ = 2*((27 - 3*1 - (-1*2) - 2*(-1))/(3² + (-1²) + 2²)) + (-1) = 2*28/14 - 1 = 3Значит, координаты точки проекции Aₒ(7;0;3).
Видео по теме