Вам понадобится
- Чертеж призмы, карандаш, линейка.
Инструкция
1
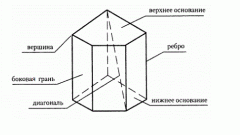
В прямой призме любое боковое ребро по определению перпендикулярно основанию. А расстояние между параллельными плоскостями боковых граней одинаково в любой точке, в том числе и в тех точках, где боковое ребро примыкает к ним. Из этих двух обстоятельств вытекает, что длина ребра любой боковой грани прямой призмы равна высоте этой объемной фигуры. Значит, если у вас есть чертеж, на котором изображен такой многогранник, на нем уже присутствуют отрезки (ребра боковых граней), каждый из которых можно обозначить и как высоту призмы. Если это не запрещено условиями задания, просто обозначьте любое боковое ребро как высоту, и задача будет решена.
2
Если требуется провести на чертеже несовпадающую с боковыми ребрами высоту, начертите параллельный любому из этих ребер отрезок, соединяющий основания. Не всегда это можно сделать «на глаз», поэтому постройте две вспомогательные диагонали на боковых гранях - соедините пару любых углов на верхнем и соответствующую им пару на нижнем основании. Затем отмерьте на верхней диагонали любое удобное расстояние и поставьте точку - это будет пересечение высоты с верхним основанием. На нижней диагонали отмерьте точно такое же расстояние и поставьте вторую точку - пересечение высоты с нижним основанием. Соедините эти точки отрезком, и построение высоты прямой призмы будет закончено.
3
Призма может быть изображена с учетом перспективы, то есть длины одинаковых ребер фигуры могут иметь на рисунке разную длину, боковые грани могут примыкать к основаниям под разными и не обязательно прямыми углами и т.д. В этом случае, чтобы правильно соблюсти пропорции, действуйте так же, как описано в предыдущем шаге, но точки на верхней и нижней диагоналях ставьте точно в их серединах.